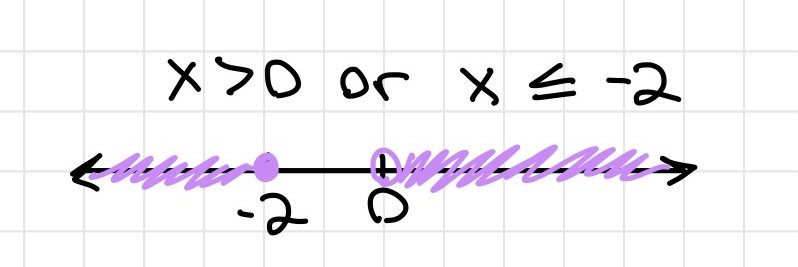
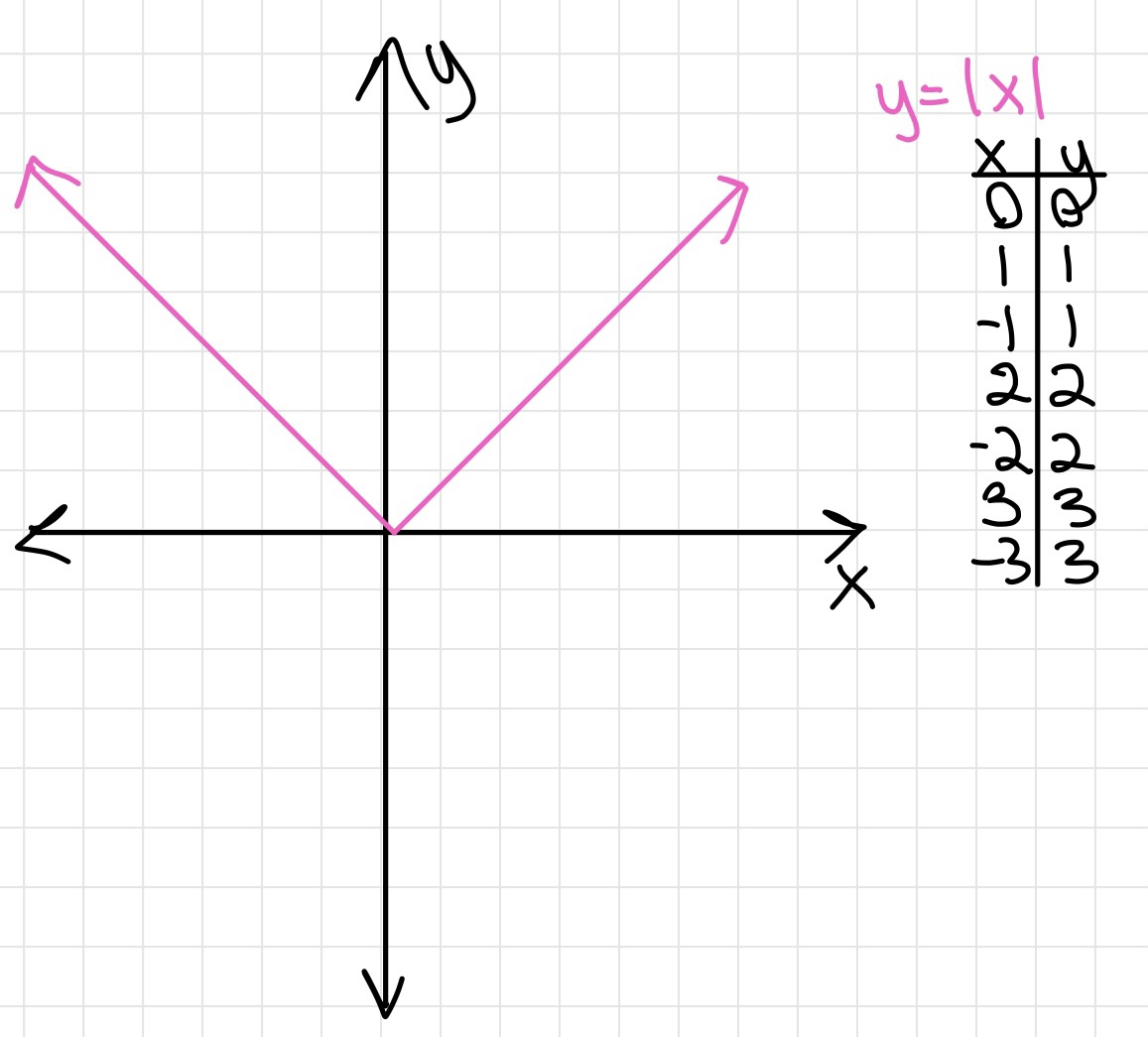
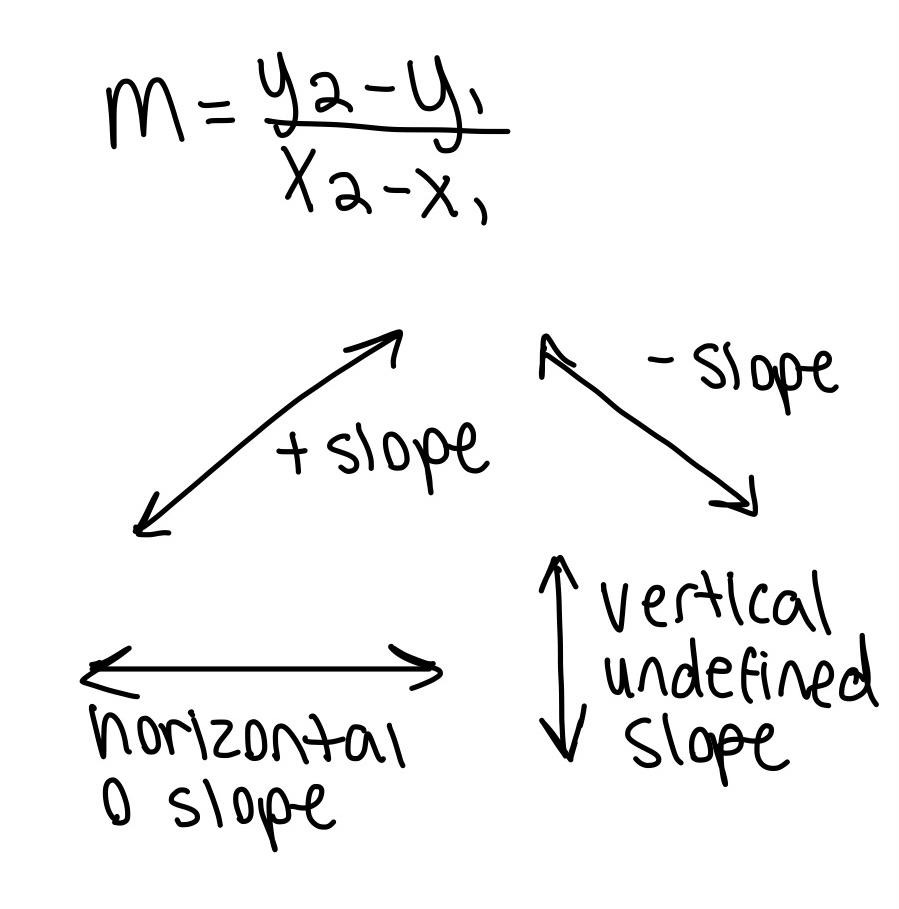
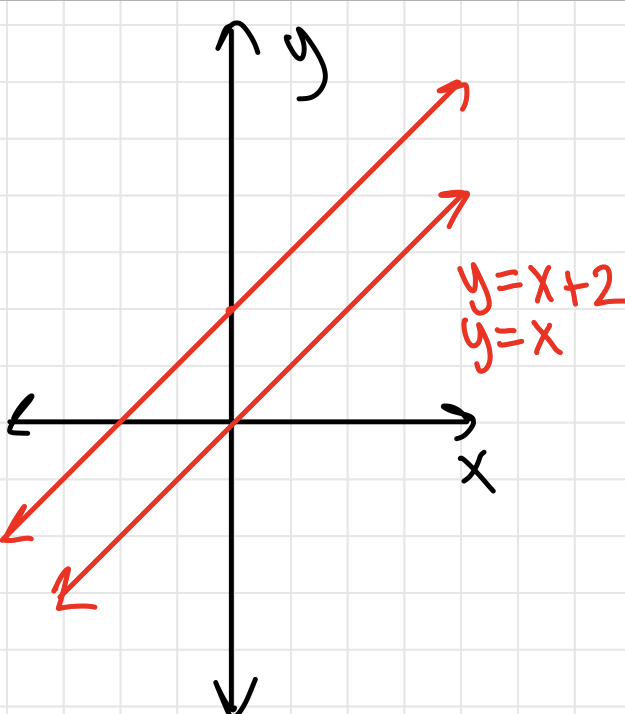
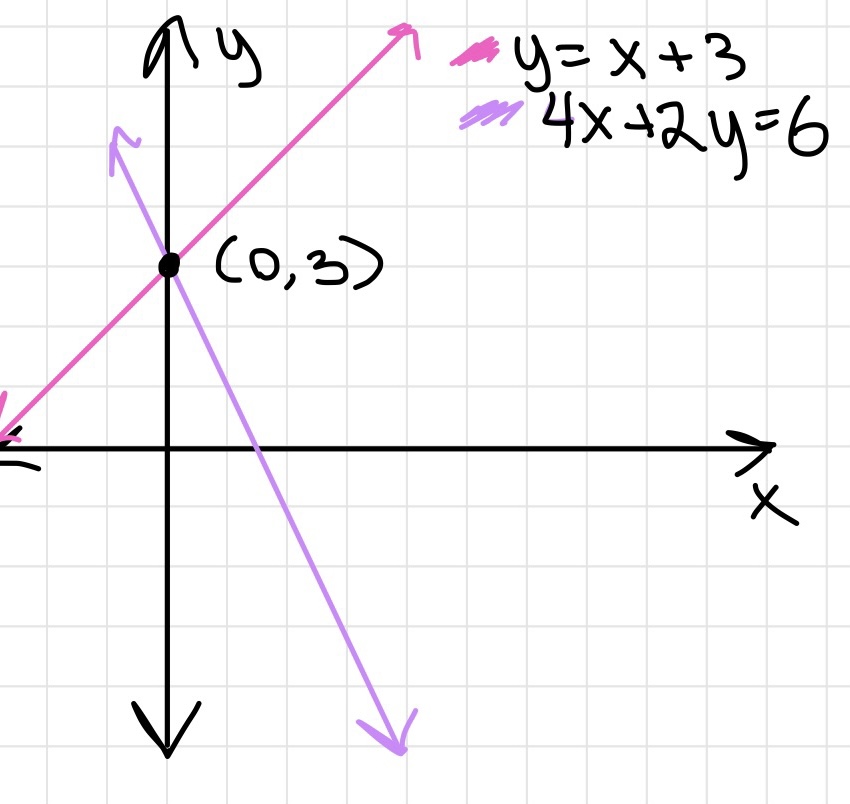
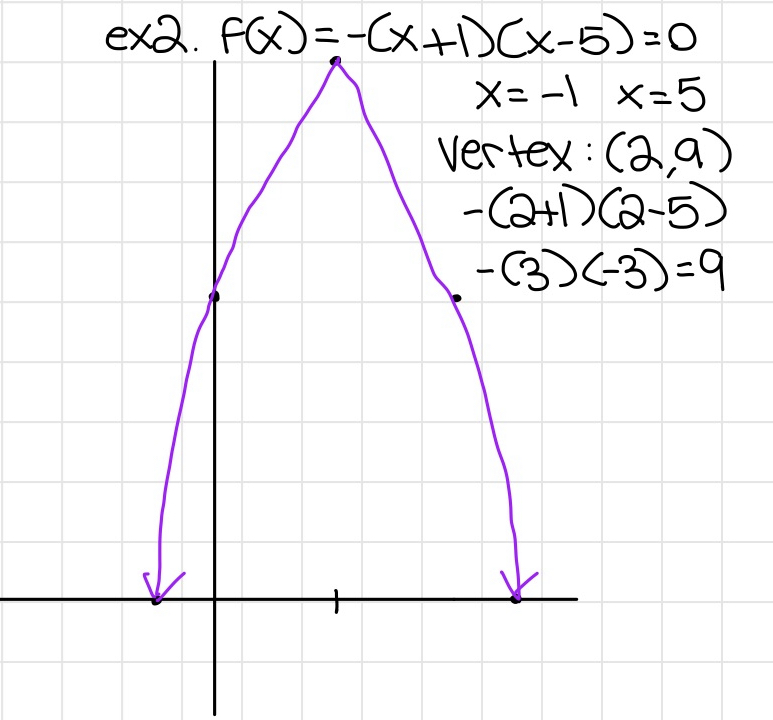
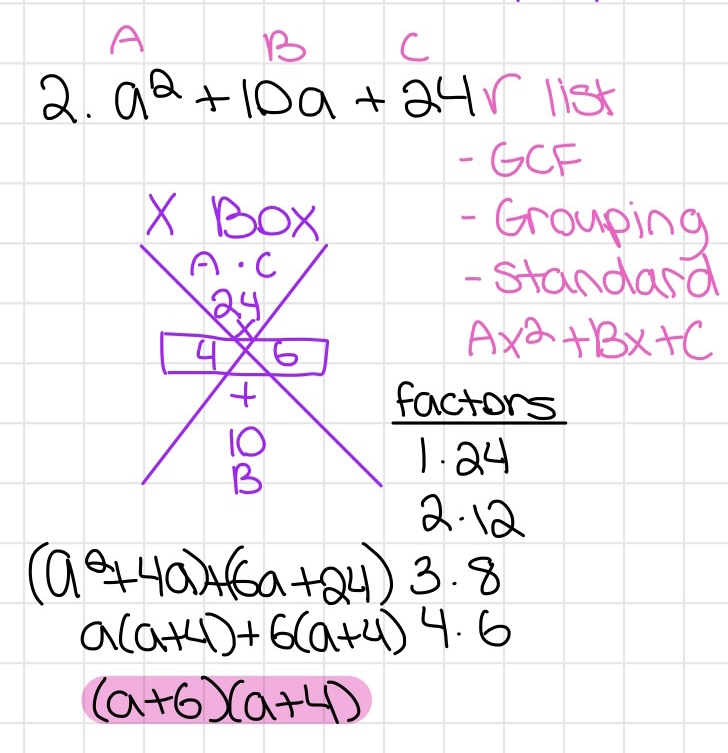
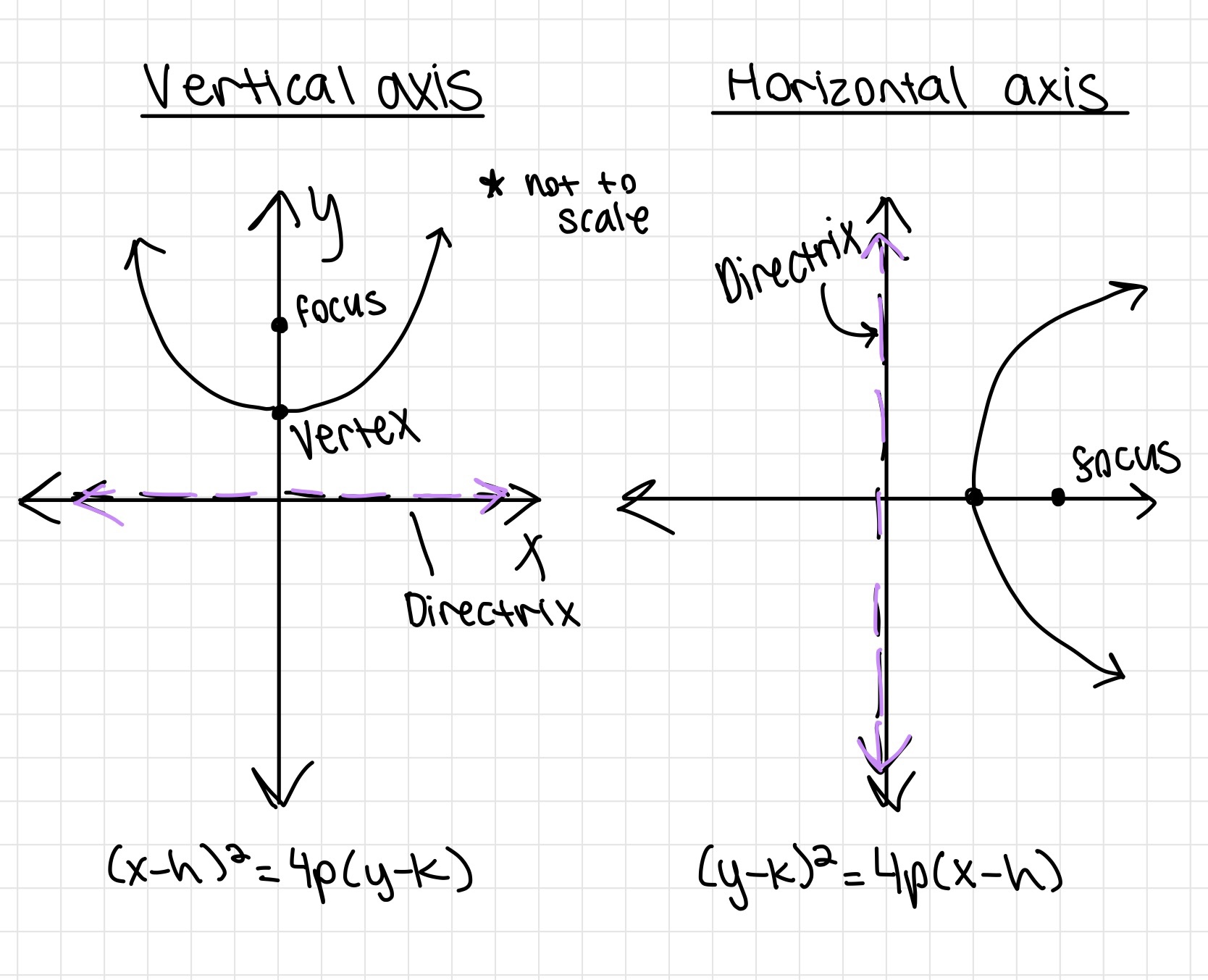
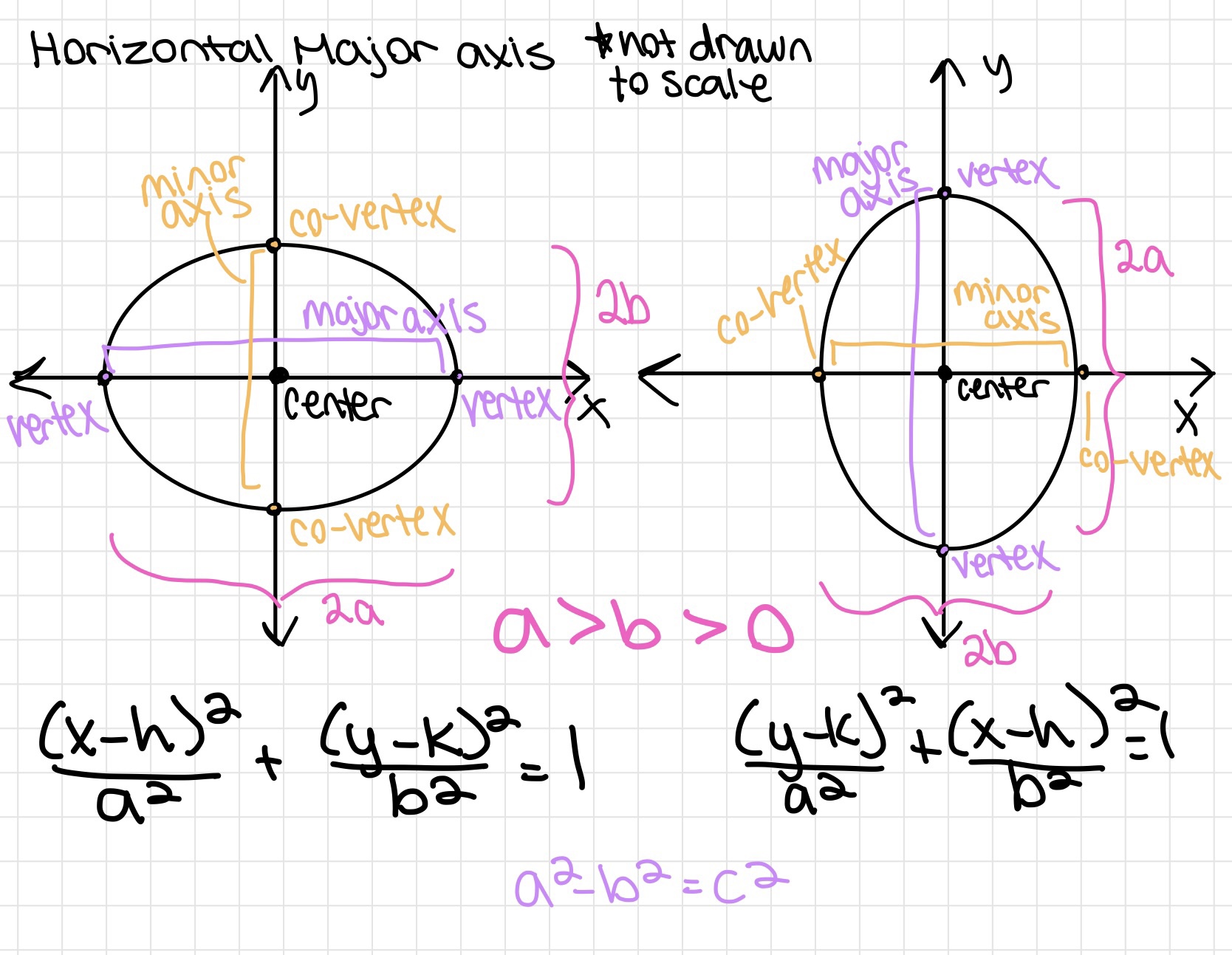
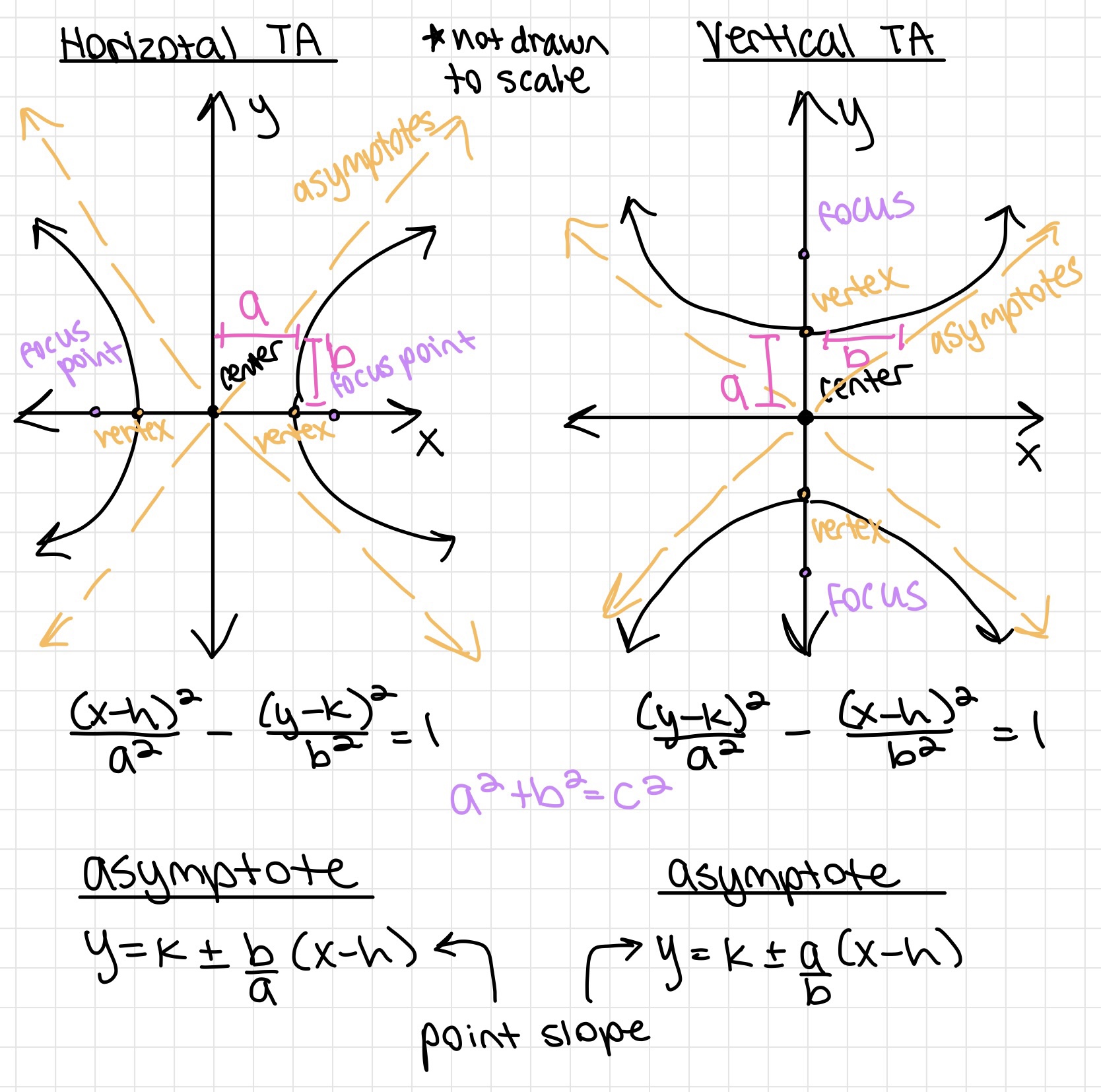
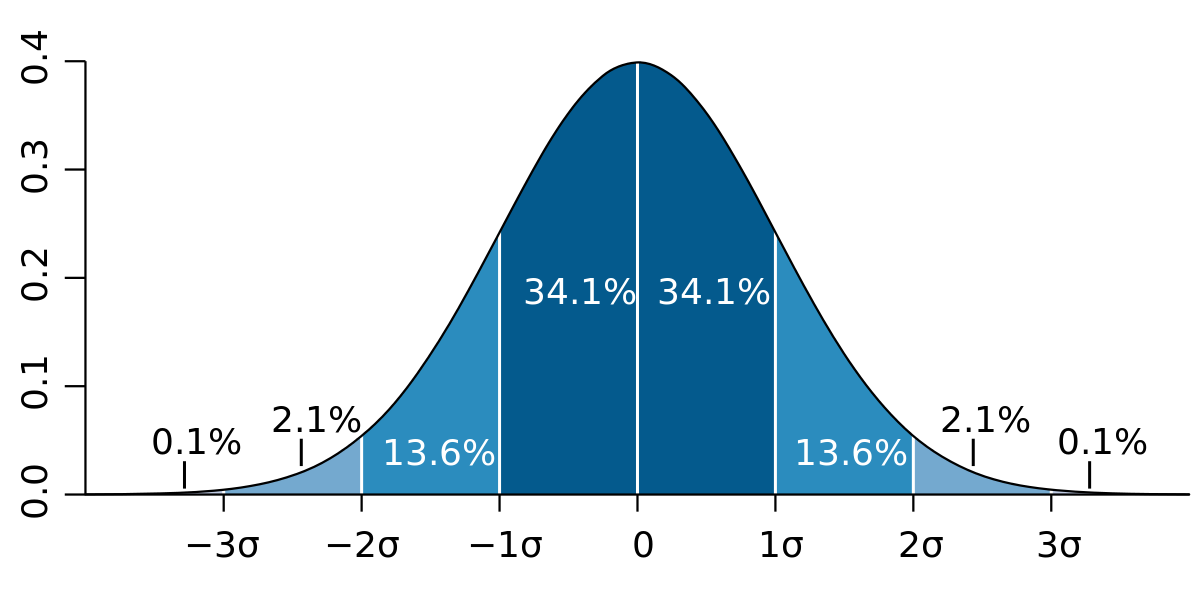
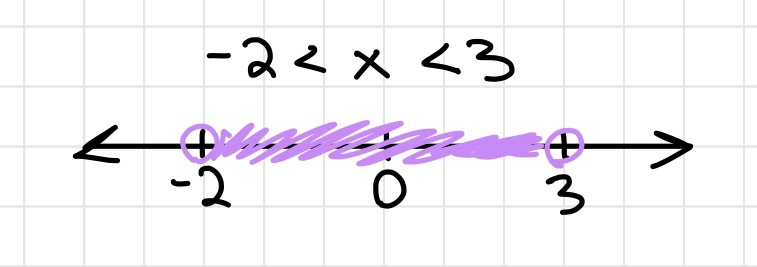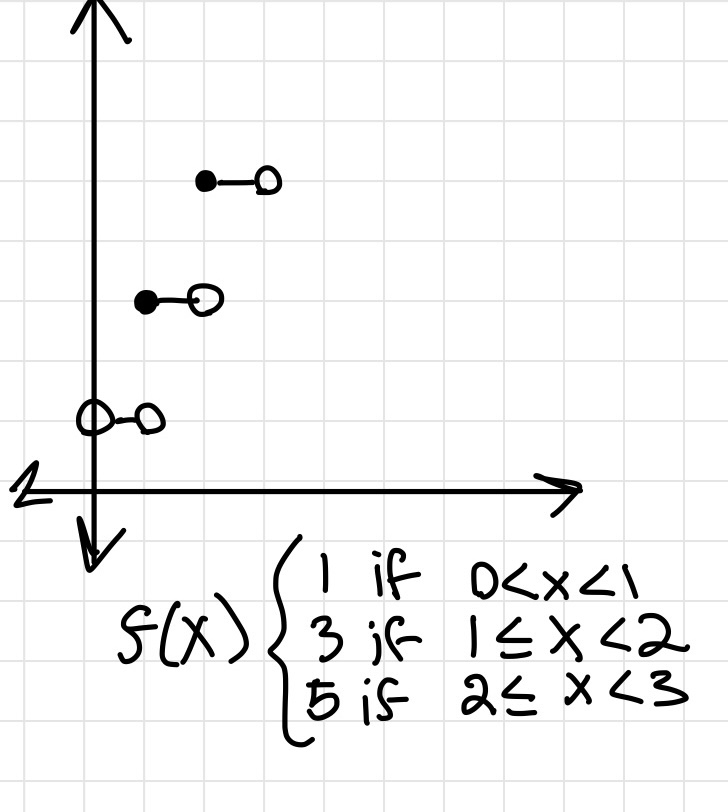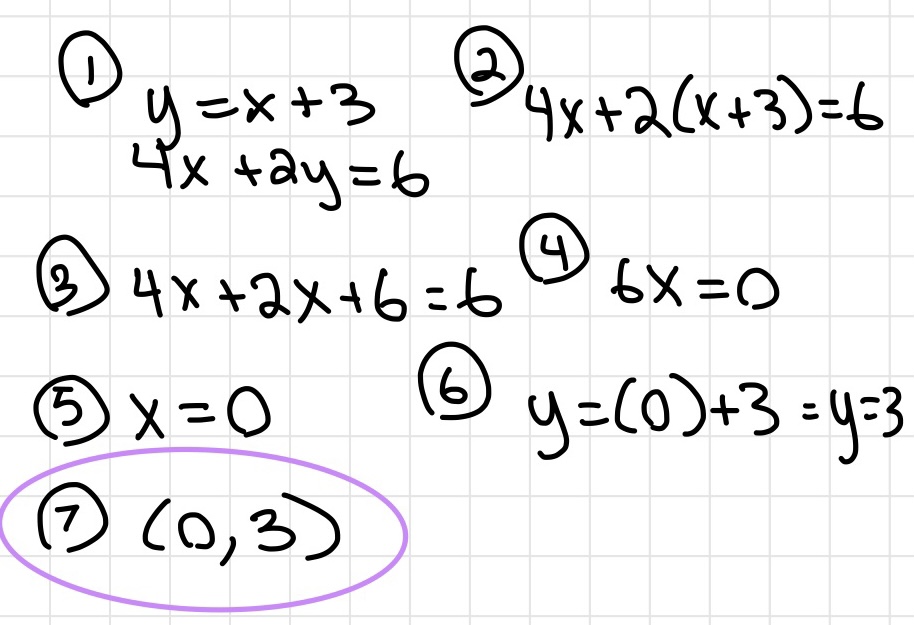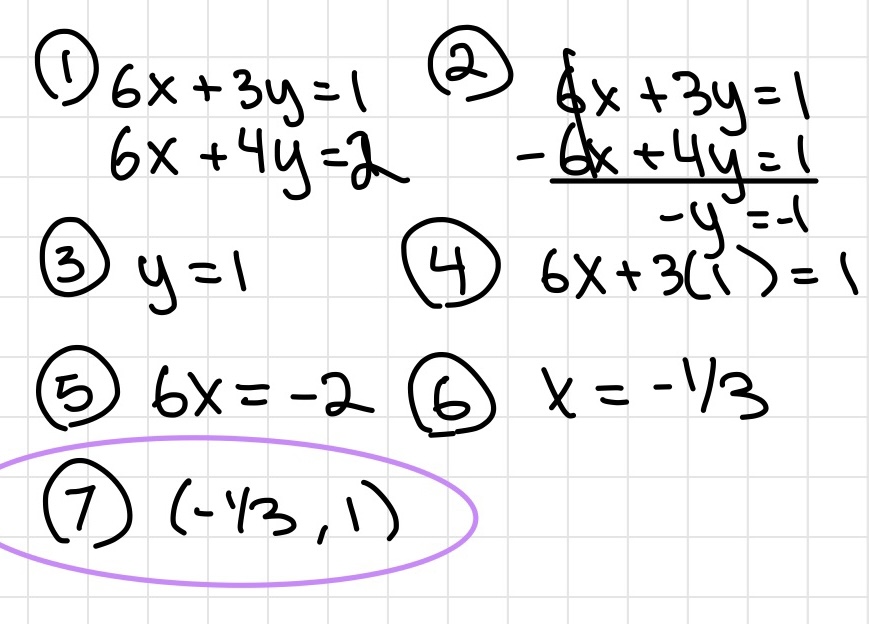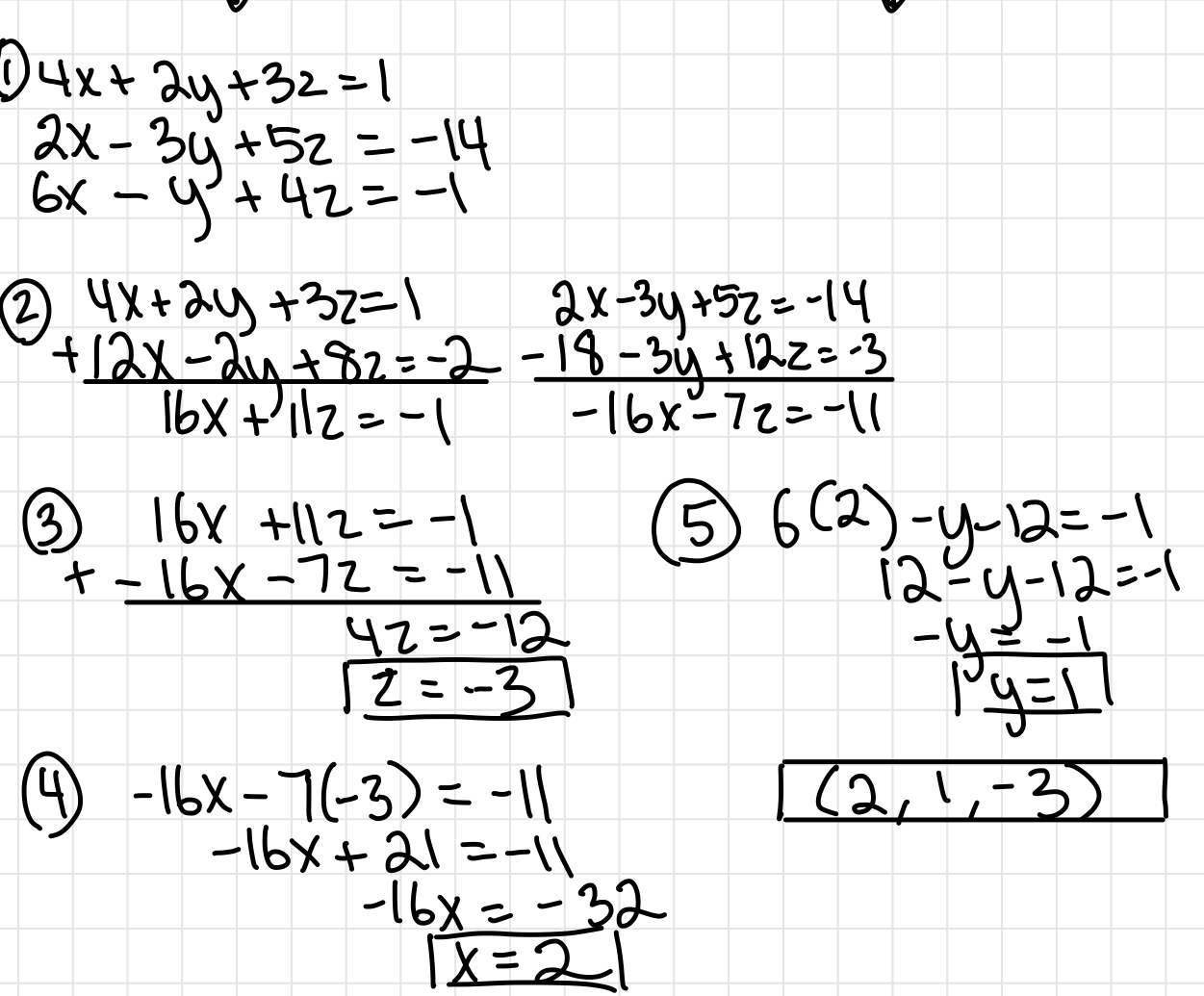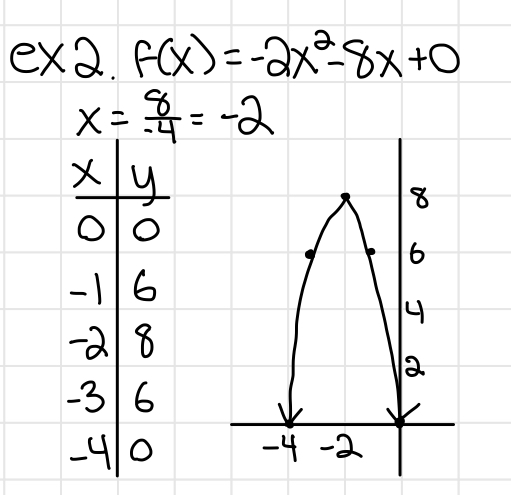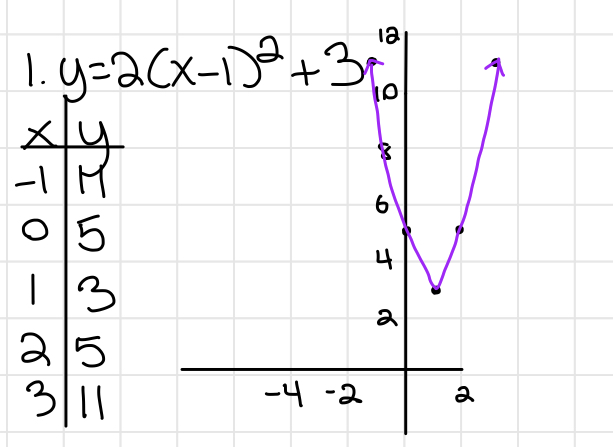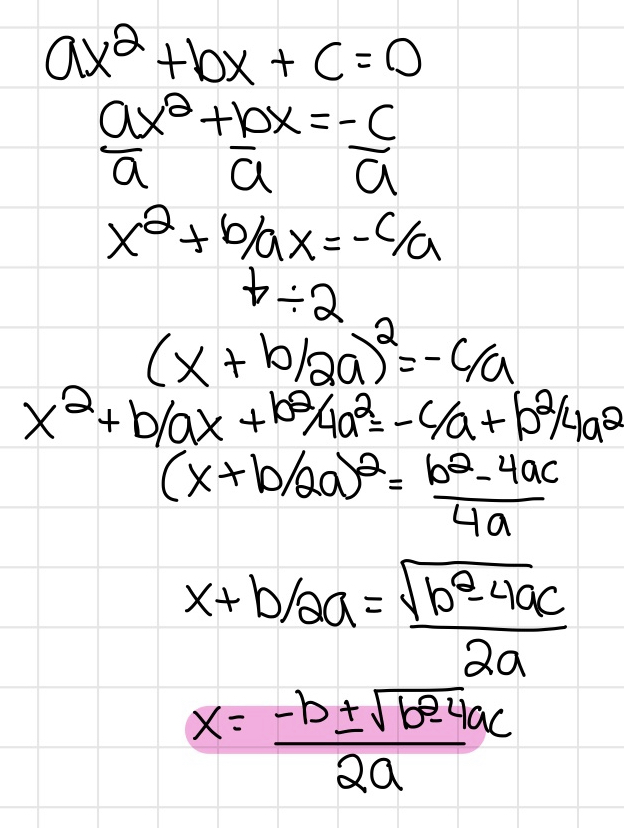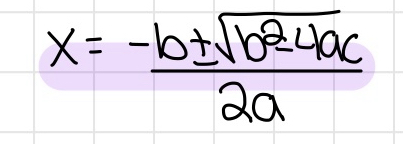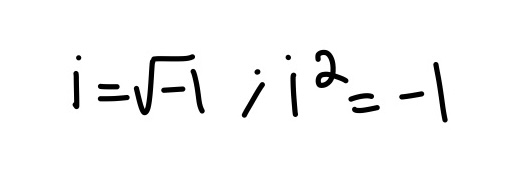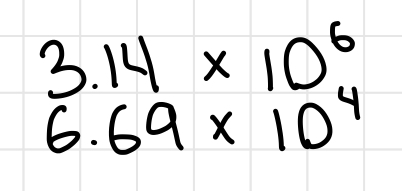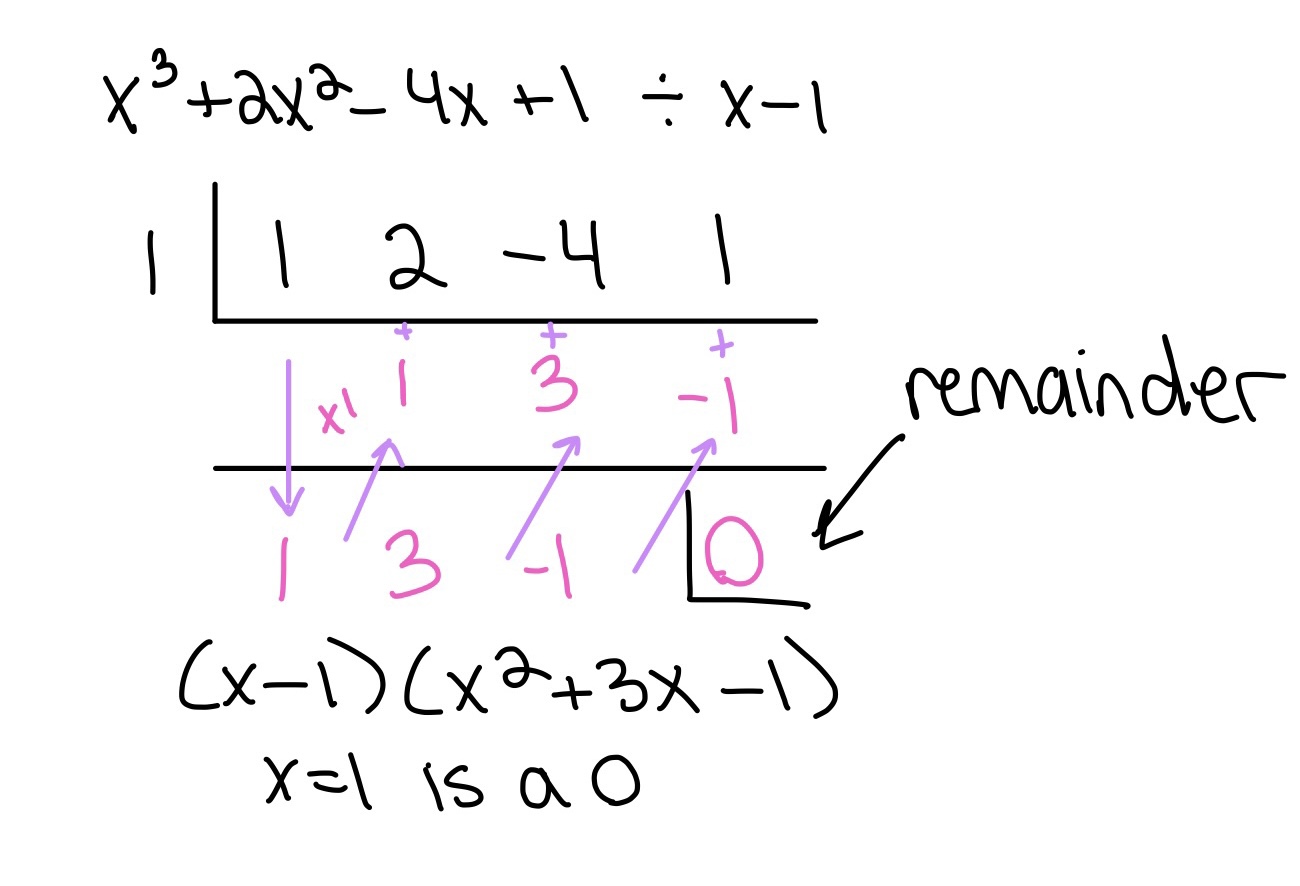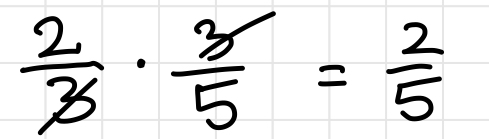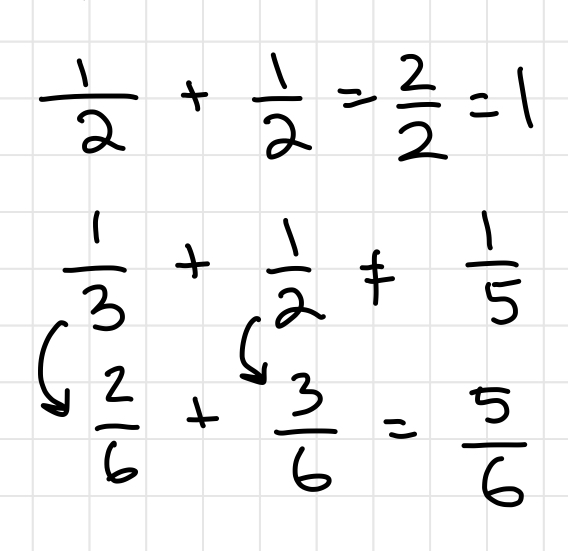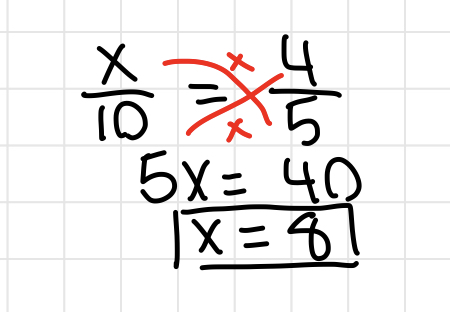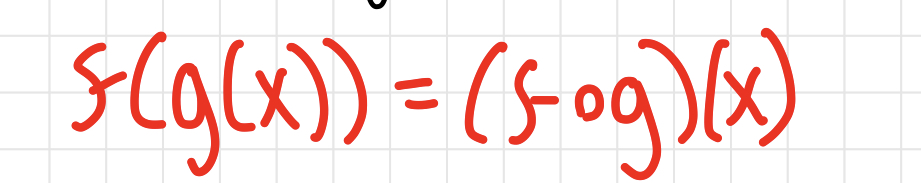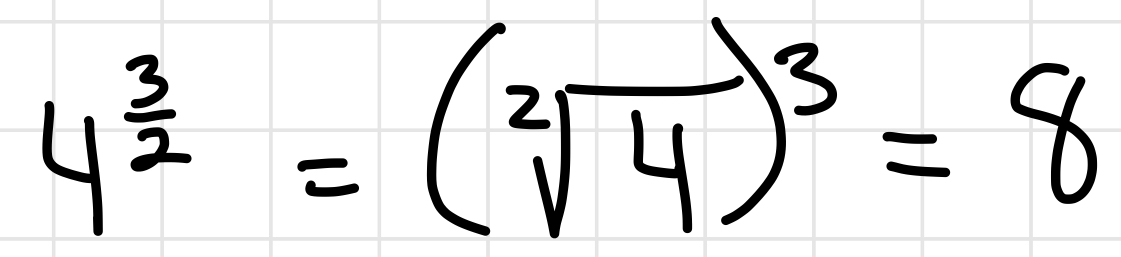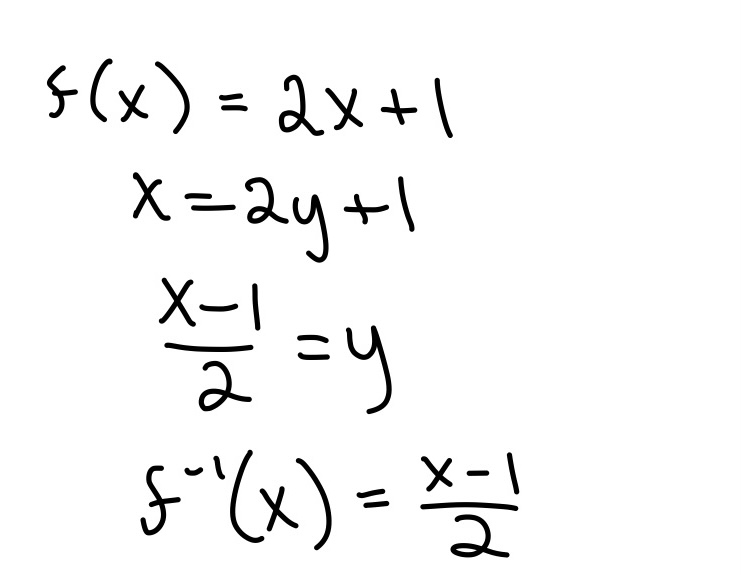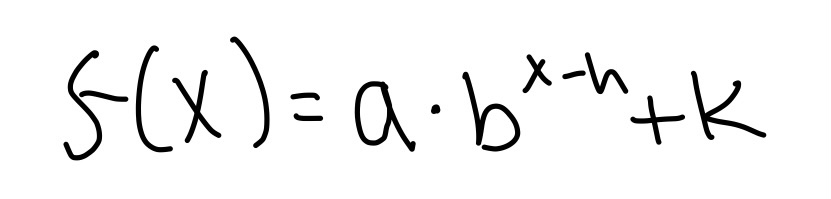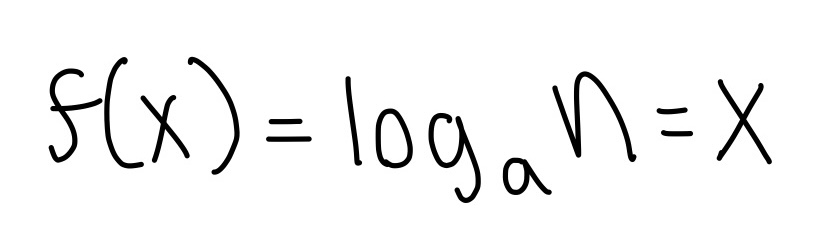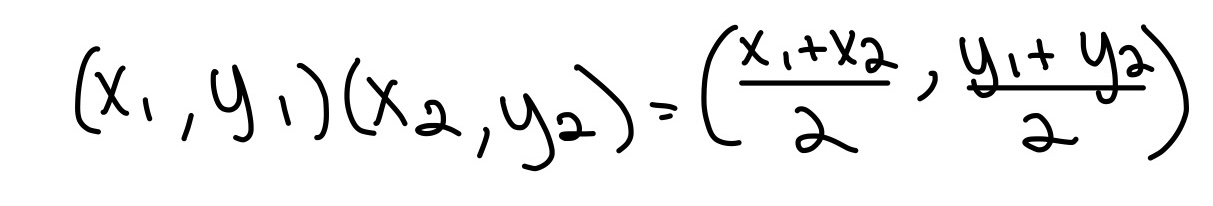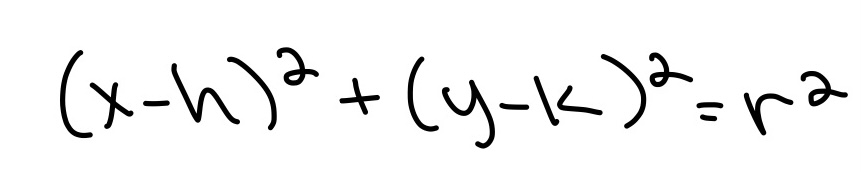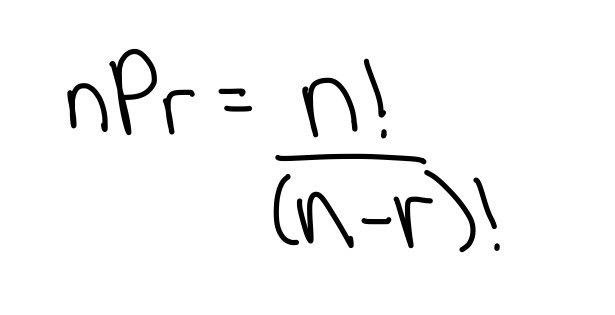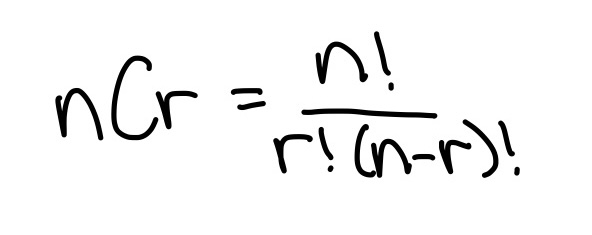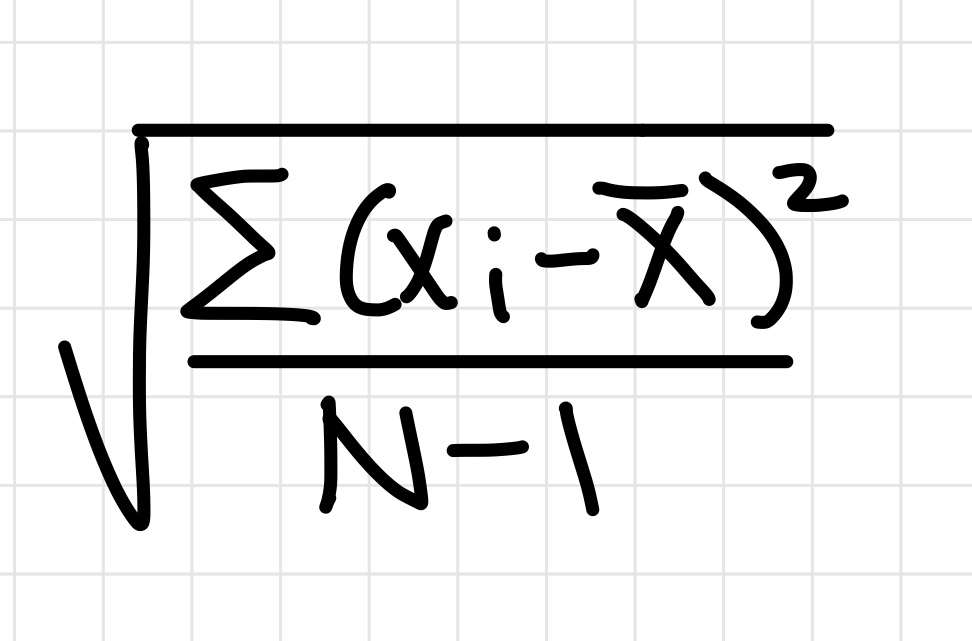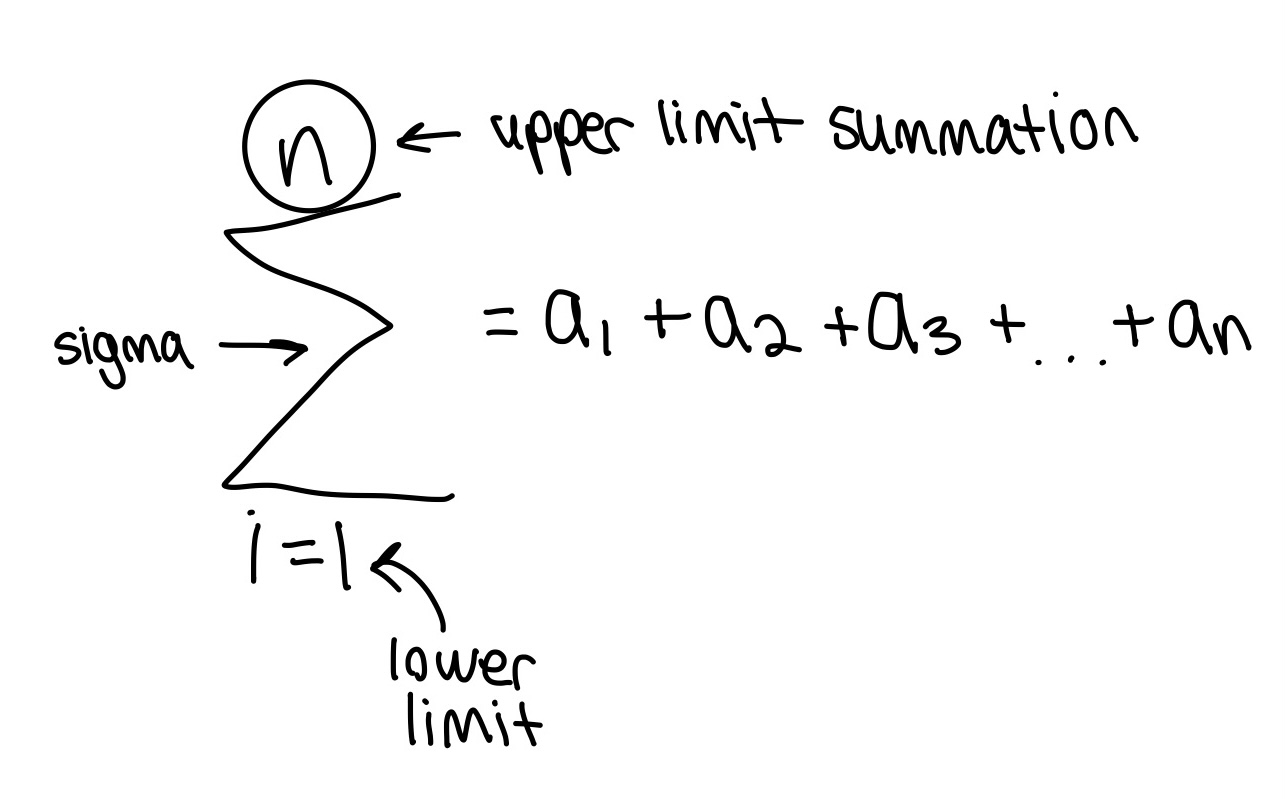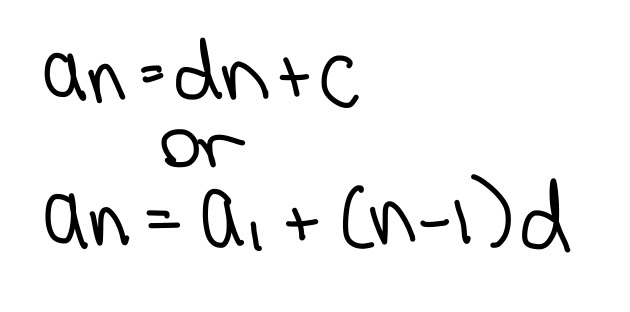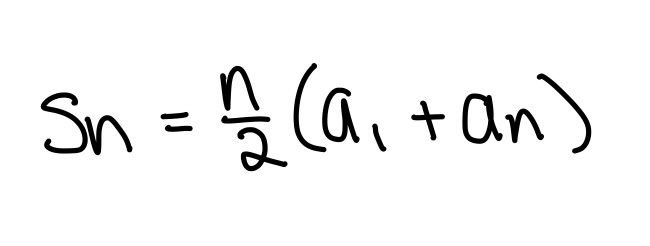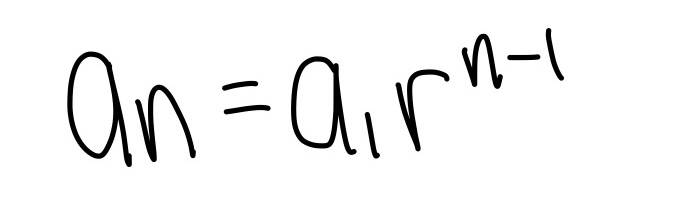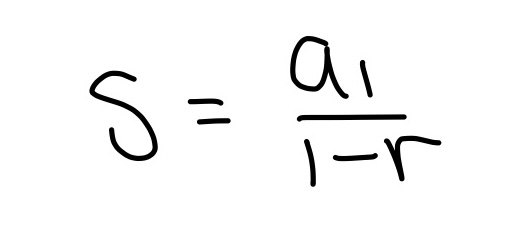~Algebra 2!~

Algebra 2 may seem scary, but don't worry, we will help you succeed :). It is similar to Algebra 1 and has a bit of Geometry, so don't sweat! You know everything. You just need a refresher

Many of the concepts in Algebra 1 are in Algebra 2 or in trigonometry. If you can't find something on this page, it is most likely on the Algebra 1 page or the Trigonometry page.

Properties

Associative Property: rearranging parantheses will not alter the answer (ex. 3 + (5 + 2) = (3 + 5) + 2)
Commutative Property: changing the order of operands does not alter the answer (ex. 2 + 5 = 5 + 2)
Distributive Property: a number next to parantheses will multiply with every number inside (ex. 3(7 + 2) = 21 + 6)
Identity Property: the answer will be the same number that was added by 0 or multiplied by 1 (ex. 2 · 1 = 2)
Inverse Property: when a number is added with itself in its opposite sign, the answer is 0 (ex. 5 + (-5) = 0)

Inequalities

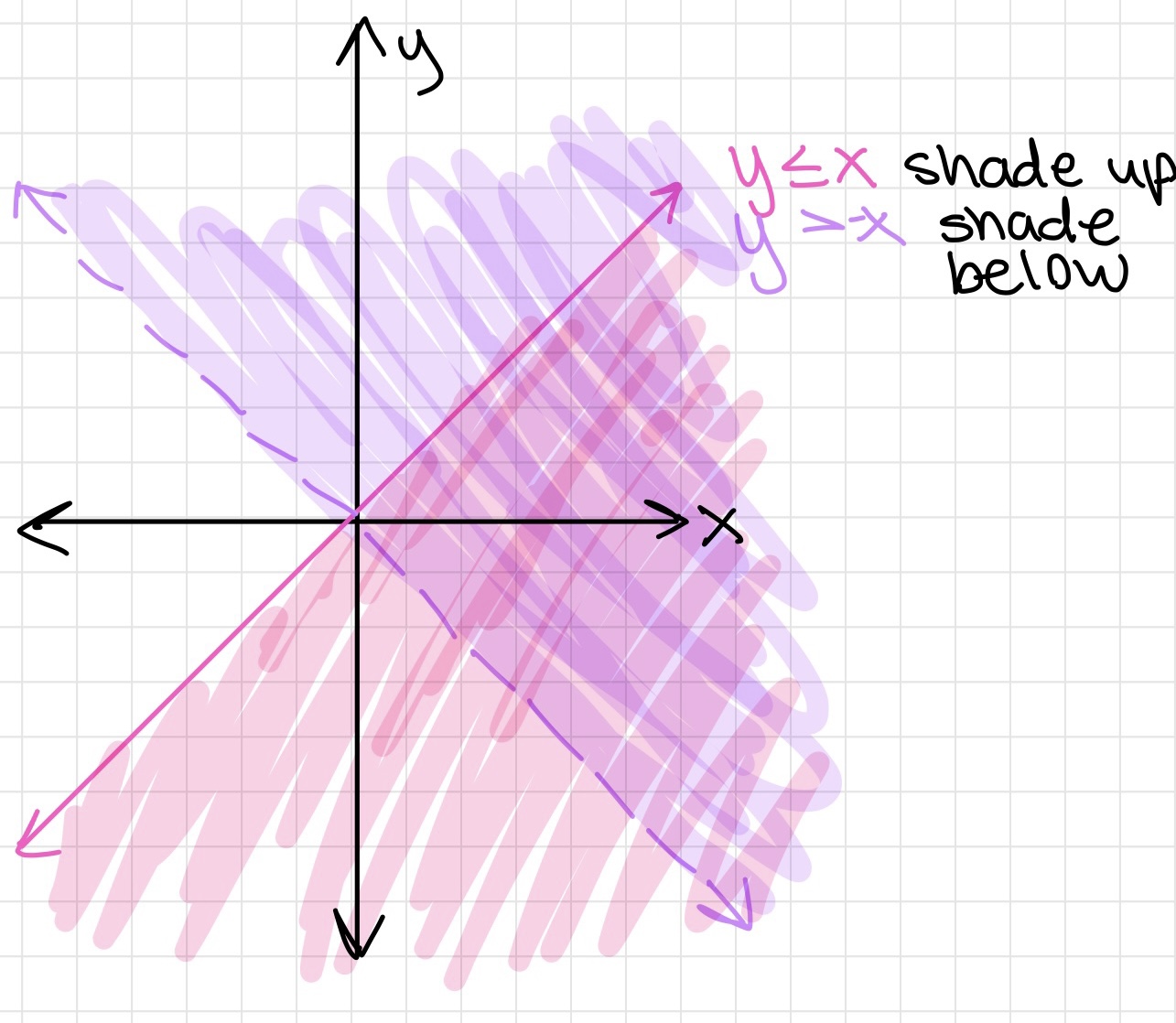
Graph of an inequality on a coordinate plane

Open and Closed Holes/Circle

An open hole/circle represents greater/less than (> <)
An closed hole/circle represents greater/less than or equal to (≥ ≤)

And

The value of x is in between two values. x has to satisfy BOTH inequalities
Ex. -2 < x < 3

Or

The value of x is NOT in between two values. x has to satisfy EITHER inequality.
Ex. x > 0 or x ≤ -2. x can't be -1 since it is not greater than 0 or less than -2.

Piecewise Functions

Step function

Multiple functions with set conditions in the form of if ___
Step function: a set of functions that make a stair-like graph

Absolute Value

Distance from 0 to the number line
Ex. |x| = 9 to -9, 9

Slope

m > 0: positive/rising slope
m < 0: negative/falling slope
m = 0: horizontal slope
m = undefined: vertical slope

Types of Lines

Parallel Lines

Same slope, different y-intercept
Aligned if a straight line is drawn vertically

Perpendicular Lines

Reciprocal slope (ex. -3 is perpendicular to -1/3)
Makes an X shape

y = mx + b

Slope in y-intercept form

ax + by = c

Standard form
For solving the y and x intercepts of the equation

y - y₁ = m(x - x₁)

Point slope form
For finding the slope equation using a point and slope (point slope form :D)

Direct Variation

y = kx
k = a number similar to m
Ex. if k = 7/2, what is y when x is 12? y = 7/2 · 12 -> 42

End Behavior/Degree

Where the ends of the graphs are heading towards
Positive end behavior: the graph is heading in the positive direction (upwards)
Negative end behavior: the graph is heading in the negative direction (downwards)
Odd degree: have origin symmetry
Even degree: have symmetry across the x or y axis

System of Linear Equations with 2 variables

Graphing

The intersection of the linear equations is the answer to the system

Substitution

Substitute one equation into the other's x or y respectively
Best used when equations in standard form are given

Elimination

Eliminate one variable to solve for the other by adding or subtracting
Best used when you can eliminate a variable by multiplying one equation with a whole number. Better yet, no multiplication is needed.

System of Linear Equations with 3 variables

Use substitution/elimination to eliminate one variable 2 times. You should have 2 new equations with 2 variables
Use the 2 equations to eliminate another variable. Solve for the remaining variable.
Plug the solved variable into one of the equations with 2 variables to solve for another variable
Use the two solved variables to solve for the last variable. Plug both of them into one of the original 3 variable equations

Polynomials

Parabola Functions

Quadratic form: ax² + bx + c
Vertex form: f(x) = a(x - h)² + k
x intercept form: a(x-p)(x-a)

Vertex in quadratic form: (-b/2a), f(-b/(2a))
Vertex in vertex form: (h, k) (when k = y and h = x)
Vertex in x intercept form: V((p+q)/2, f((p+q)/2))

A few notes:

a² + 2ab + b² = (a + b)²
(a + b)(a - b) = a² - b²

Quadratic Formula

Used to find the zeros of the binomials
When a trinomial isn't factorable, use the quadratic formula to get the exact answers

X Box Method for Factoring

Put "a · c " at the top of the X and "b" at the bottom of the X
Find two numbers that multiply to "a" AND add up to "b"
One they are found, make two binomials like this: (ax² + 1st number)(2nd number + c)
Take out a common factor for each binomial.
If the binomial in the parantheses are the same, which they should be, put the factors into their own binomial in parantheses.

Radicals

Index: how many times a number is multiplied to get the radicand
Radicand: the number inside the root

Imaginary numbers

i = √-1; i² = -1

Complex Conjugates

Complex conjugates: a + bi and a - bi
Ex. the complex conjugate of 2 - 3i is 2 + 3i
Multiply by the complex conjugate of an imaginary fraction to simplify it

Standard form

a√b i
|a + bi| = √(a² + b ²)

Properities of exponents

Product of powers: 2³ · 2² = 2⁵ = 32
Power of a power: (2³)²
Power of a product: (2xy)³ = 8x³y³
Negative exponent: (2/5)^-2 = 25/4 (Negative exponents flip the numerator and denominator)
Zero exponent: (20000)⁰ = 1
Quotient of powers: x⁵/x² = x³
Power of a quotient: (x / y) ²

Scientific Notation

0 < # < 10 · 10 ^#
Makes large numbers easier to read
The exponent is the amount of times the decimal pont moves backwards/forwards. Add zeros for the extra digits.
If the exponent is negative, move the decimal point backwards.
If the exponent is positive, move the decimal point forwards.

Synthetic division + Possible Rational 0s

Possible rational 0: values of x that could make the equation equal to 0
For convenience: pr0 = possible rational 0
If a pr0 provides a -remainder and another pr0 provides a +remainder, the actual rational 0 will be a value in between them
Ex. 1 and 3 are pr0s. 1 = -8 as a remainder and 3 = 48 as a remainder; 2 is the rational 0 in between 1 and 3 that will produce a remainder of 0

Factoring Fractions

The same numbers on the numerator and denominator can be cancelled out (since dividing a number with itself = 1)

Adding and Subtracting Complex Fractions

If two denominators are the same, you can add and subtract the fractions
If the two denominators ARE NOT the same, find the least common denominator between the two fractions. Multiply the fractions by a number over itself to get the desired denominator.
If you multiply on one side, multiply on the other side.

Proportions

Cross multiply to solve for x

f(x)

Pronounced f of x
Essentially y
The function f at x has a specific y value

Composition of functions

A function becomes the x of another function
Can be written in this notation

Rational/radical exponents

Example of an exponent as a fraction

Rational number: a number that can be written as a fraction
The denominator of a radical exponent is what the root will be (ex. x^1/2= √x
The numerator of a radical exponent is what the number will be raised to the power of (ex. x^3/2= (√x)³

Inverse Functions

IS NOT 1/f
Swap x and y then solve for y to find the inverse function
If you are trying to find the inverse of a parabola, make sure to find the restriction

Logarithms, Exponentials, and Compound Interest

Exponentials

Has a horizontal asymptote
Focal point: first integer point closest to HA
a: distance between focal point and horizontal asymptote (+ = focal point is above HA, - = focal point is below HA)

Logarithms

Has a vertical asymptote
logX: log₁₀X
lnX: log_eX
log_an = x is the same as a^x = n
log_an = x is the same as ln n / ln a = x

Distance Formula

Finds the distance between two points on a coordinate plane
The distance formula is also the pythagorean therom.
The distance between two points is the hypotenuse of a right triangle.

Midpoint Formula

Finds the middle point in between two points on a coordinate plane
Dividing by two finds the center x and y point

Conic Sections

Parabolas

p = distance between the vertex and focus point
h = changes the x position of the vertex
k = changes the y position of the vertex
The directrix is always behind the parabola's vertex
The focus is always directly in front of the vertex

Ellipses

h = changes the x position of the center
k = changes the y position of the center
a = distance between the center and vertex
b = distance between the center and co-vertex
c = distance between the center and focus (the focus is directly in front of the vertex)

Hyperbolas

h = changes the x position of the center
k = changes the y position of the center
a = distance between the center and vertex
b = distance between the center and co-vertex
c = distance between the center and focus (the focus is directly in front of the vertex)
There are two asymptotes that cross each other at the center

Equation of a Circle

Center = (h,k)
Radius = r
Find the midpoint of the circle using two points to find the center
Distance from a point and the center is the radius

Probability

Factorials

Represented by n!
Multiply by every number leading up to n
Ex. 5! = 1 · 2 · 3 · 4 · 5
Used for combinations and permutations

Notes

Use these notes when assessing how to solve the probability of a scenario
Adding (+): you have a choice/or
Multiplying (·): calculate probability/and
n = total amount of items in a scenario (refer to the two images below)
r = amount of positions/number of objects to choose (refer to the two images below)

Permutation

Use permutations when the order in a scenario matters
Ex. How many ways can a group of people come in 1st, 2nd, and 3rd place

Combination

Use combinations when the order in a scenario DOES NOT matter
Ex. Pick 4 meals out of a menu with a total of 15 meals

Odds in favor/not in favor of an event

Binomial Theorem

Use the triangle above to expand a binomial by its respective exponent
Multiply each term in the expansion according to the triangle
First row: exponent = 0
Second row: exponent = 1
Third row: exponent = 2
Fourth row: exponent = 4. etc.

Example

Expand (2x + 3y) ⁴
Binomial is to the power of 4
1(2x)⁴ (3y) ⁰ + 4(2x)³(3y)¹ + 6(2x)²(3y)² + 4(2x)¹(3y)³ + 1(2x)⁰(3y)⁴
Simplify

Data terms

Mean: average; find by adding all the data and divide by the total numbers present
Median: the middle of the data set
Mode: most common number in a data set
Range: largest - smallest

Standard deviation:

Σ = sigma: sum of multiple terms
N = sample size
x _i = each value from the data set
x with the line above: mean

Standard Deviation Bell Curve

Shows how common a certain part of the data is
Used in biology if you are taking that

Arithmetic and Geometric Sequences

n

Represents the term of a number in a sequence. Essentially where the number is in a sequence.

Summation Notation

Easy way to write a summation of a sequence
n = the amount of times the right side is added to itself (represents the last term of the sequence)
i = contributes to the amount of times the right side is added to itself (represents the first term of the sequence)
If i does not equal 1, the sequence starts at another place in the sequence

Infinite Sequence

A sequence that goes on infinitely. n = infinity
Partial sum: a limit (n) is set on the infinite sequence.
Infinite series: sum of all terms in an infinite series

Arithmetic sequences

Finds the nth term of a sequence. Has LINEAR nth term rules (addition/subtraction).
d = common difference (pattern in the sequence). Ex. add 6 for each term
The bottom formula is the same as point slope form

Used to find d in an arithmetic sequence. You can use d to find the arithmetic equation of the sequence
Same formula used to find the slope of a line
Numerator: subtract the two numbers
Denominator: the subtraction of the nth term of both numbers

Efficient way to find the sum of the first n terms of an arithmetic sequence

Geometric Sequences

Finds the nth term of a sequence. Has EXPONENTIAL nth term rules (addition/subtraction).
r = common difference (pattern in the sequence). Ex. add 6 for each term

Finds the sum of the first n terms of a geometric sequence

Finds the sum of an infinite geometric series