Intro to Limits
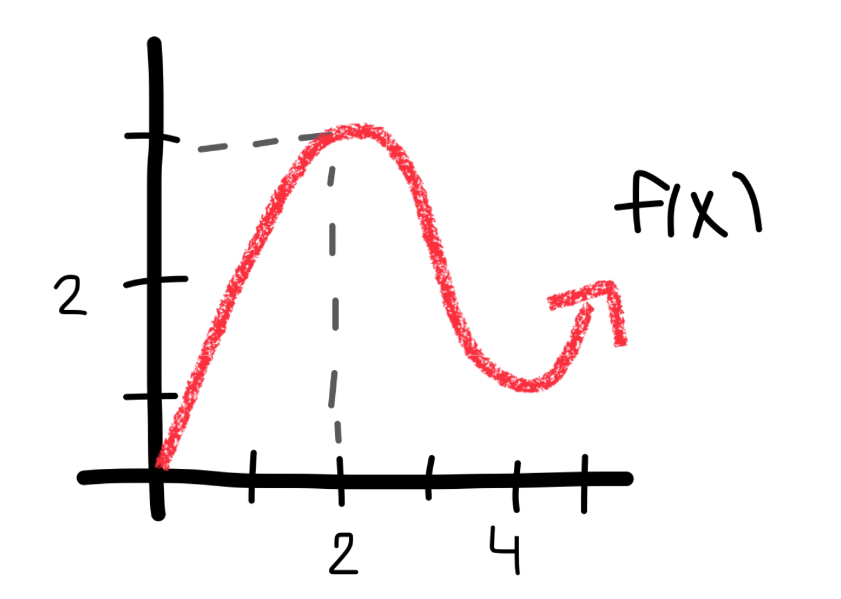
as x gets closer to 2 x → 2
f(x) gets closer to 3 f(x) → 3
∴ lim f(x) = 3
say: limit as x approaches 2 of f(x) is 3
Okay so Calculus seems scary....and IT IS. We're kidding, once you get the hang of it, it'll be alright! Just try your best and don't give up.
When first starting off Calculus, you should know these important equations... Derivatives and Integrals!
Here is a link to all the Need Statements you should know, they're basic formulas and statements everyone should memorize when doing Calculus.
Also here are two other important links to use to review for the AP test! Theorems & Trignometry. Bound to get a 5 for sure.
These are all the notes we were able to type out so far, of course there is so much to Calculus AB so please do check out the documents pasted above which has a whole summary of the calculus that may come on the AP test! If youw ant more complex and extra explanations use resources like Organic Chemistry Tutor, Khan Academy, and Paul's Online Notes, they wil be your best friends.
- symmetry to y-axis is an even function so f(-x) = f(x)
- symmetry to origin is an odd function so f(-x) = -f(x)
- symmetry to x-axis is neither even or odd so -f(x) = f(x)
ex. y = g(x) = cosx/(x4 + 1)
g(-x) = cos(-x)/((-x)4 + 1) = cosx/(x4 + 1) = g(x)
so g(x) is symmetric to the y-axis
domain: is the set of all possible x-value inputs
range: is the set of all possible outputs y-value
ex. y = 1/(x2 - 3x + 2)
domain: denominator ≠ 0
(x-2)(x-1) ≠ 0
x ≠ 1, 2
(-∞, 1)∪(1, 2)∪(2, ∞)
range: (-∞, 0)∪(0, ∞)
basic types of transformations (c > 0)
original graph f(x)
horizonal shift c units right
f(x-c) *horizontal, c is inside the function*
c units left f(x+c)
vertical shift c units up f(x)+c *vertical, c is outside the function*
c units down f(x)-c
reflection x-axis -f(x)
reflection y-axis f(-x)

as x gets closer to 2 x → 2
f(x) gets closer to 3 f(x) → 3
∴ lim f(x) = 3
say: limit as x approaches 2 of f(x) is 3
h(2) = does not exist
∴ lim h(x) = 3
limit exists at holes
∴ lim g(x) = -2 ∴ lim g(x) = 1
∴ lim g(x) = DNE ∴ lim g(x) = -1
∴ lim g(x) = +∞ ∴ lim g(x) = -∞
def: a rational function is a function of the form r(x) = p(x)/q(x)
where p(x) & q(x) are polynomial functions & q(x) ≠ 0
to graph:
- find holes first, factor, & cancel
- zeros: let numerator = 0 solve for x
- y intercepts: let x = 0 solve for y
- vertical asymptotes: let denom = 0
- horizontal asymptotes: deg. num ≤ deg. of denom
- slant asymptote: deg num = 1 + deg. denom
- if deg. num > 1 + deg. denom there is no asymptote
- make sure to find holes before vertical asymptotes
- check for symmetry & then GRAPH! keep practicing how to graph...
to find infinte limits w/o graphing: lim when x → a ± p(x)/q(x) = ±∞ if & only if
lim when x → a ± p(x) = non-zero constant & lim when x → a ± q(x) = 0
to find infinte limits w/o graphing: lim when x → ±∞ C/xn = 0
goal is to rewrite the function to produce expressions C/xn
multiply numerator & denominator by 1/xhighest power of denom.
if f is contonuous on [a, b] and if f(a) ≠ f(b), then for any # k between f(a) & f(b) there exists at least one # c between a and b such that f(c) = k
ex. f(x) = x3 - x2 + x -2 [0,3] f(x) = 4
✓ f is continuous on [0,3]
✓ f(0) ≠ f(3)
✓ f(0) < 4 < f(3)
c3 - c2 + c - 2 = 4
c3 - c2 + c - 6 = 0
(c-2)(c2 + c2 + 3) = 0
a = 0 < c = 2 < b = 3
∴ intermediate value thm applies
def: the derivative of f(x) at only pt x is
f'(x) = lim f(x + ∆x) - f(x) / ∆x
alternate def: derative of f(x) at x = c
f'(x) = lim f(x) - f(c) / x - c
derative = slope of a tangent line = instantaneous rate of change
f'(x) *say f prime of x*
y' *say y prime*
dy/dx *say dee y dee x*
constant rule: d/dex [c] = 0
power rule: d/dx [xn] = nxn-1
constant multiple rule: d/dx[cf(x)] = c ⋅ f'(x)
sum & difference rule: d/dx [f(x) ± g(x)] = f'(x) ± g'(x)
product rule
if h(x) = f(x) ⋅ g(x)
then h'(x) = f'(x)g(x) + g'(x)f(x)
think it this way: deriv of 1st times 2nd plus deriv of 2nd times 1st
quotient rule
if h(x) = f(x) / g(x)
then h'(x) = f'(x)g(x) - g'(x)f(x) / [g(x)]2
think it this way: deriv of the top times the bottom minus deriv of bottom times the top all over the bottom squared
original: f(x) 1st deriv: f'(x) 2nd deriv: f''(x)
product rule
if h(x) = f(x) ⋅ g(x)
then h'(x) = f'(x)g(x) + g'(x)f(x)
think it this way: deriv of 1st times 2nd plus deriv of 2nd times 1st
quotient rule
if h(x) = f(x) / g(x)
then h'(x) = f'(x)g(x) - g'(x)f(x) / [g(x)]2
think it this way: deriv of the top times the bottom minus deriv of bottom times the top all over the bottom squared
particle moving horizontally or vertically
position function: s(t) or x(t) or y(t)
velocity: v(t) = s'(t)
accerlation: a(t) = v'(t) = s'(t)
average velocity Δs/Δt = change in position/change in time
particle changes direction v(t) changes sign
total distance traveled from t = t1 to t = t2
DT |s(t1) - s(tc)| + |s(tc) - s(t2)|
tc = time particle changes direction
basically you solve for dy/dx
ex. derative of y2 is 2y ⋅ dy/dx
related rates is to find the rates of chnage of 2 or more related variables that are changing with the respect to time
ex. when water drains out of a conical tank the volume V, the radius r, and the height of the water h are all functions of time
V = 1/3 ⋅ πr2h
dv/dt = 1/3 ⋅ π[2r ⋅ dr/dt ⋅ h + dh/dt ⋅ r2]
bsically determind what you are looking for, when this is occuring, and what you are given
then make a sketch, label variables, write an eq relating to them, differentiate implicty with respect to time
finally substitute known values!
Just check out the Theorems
Okay so honestly, if you take a look at the Needs Statements page, you will be able to solve each one of these problems
y = logbx, b > 0 ⇔ x = by
y = logb(xy) = logb(x) + logb(y)
y = logb(x/y) = logb(x) - logb(y)
y = logb(xy) = ylogb(x)
y = logb(ysqrt(x)) = 1/y ⋅ logb(x)
ALSO:
elnx = x
ln(ex) = x
use ln as an aid in differentation in non-ln properties
take ln of both sides
the inverse function is denoted as f-1 (f inverse)
ex. y = sqrt(2 - 3x)
x = sqrt(2 - 3y)
x2 = 2 - 3y
3y = 2 - x2
y = 2 - x2 / 3
f-1(x) = 2 - x2 / 3
it's done to solve indeterminate form of 0/0 or ∞/∞
basic rule is you take the derivative of the top and bottom seperately to solve!
.png)
ex. y = sin(3x)
dy/dx = cos(3x) ⋅ 3
∫dy = ∫cos(3x)3dx
y = 1/3 ⋅ 3sin(3x) + C
∫xsqrt(2x-1)dx
= ∫(u+1)/2 ⋅ u1/2 du/2
= 1/4∫u3/2 + u1/2 du
= 1/4[2/3 ⋅ u5/2 + 2/3 ⋅ u3/2]
= 1/4[2/15 ⋅ u3/2 (3u + 5)
= 1/30 ⋅ (2x-1)3/2 (3(2x-1) + 5)
= 1/30 ⋅ (2x-1)3/2 (6x-3) + 5)
u = 2x - 1
x = (u + 1) / 2
dx = 1/2 ⋅ du
the rate of change in temp of an object is proportional to the difference between the object's temp & the temp of the surrounding medium
y = temp of object & ys temp of surrounding medium SO... dy/dt = k(y - ys)
area between curves = ∫ (top curve) - (bottom curve) dx
the bottom bound is left
the top bound is right
∫udv = uv - ∫vdu
repeated integration by parts: ∫xnsin(ax)dx, ∫xncos(ax)dx, ∫xneaxdx