Line Segments and Distance
- def: a line segment consists of the end pts of the segement and all the points between the endpoints
- def: Q is between A and B if and only if A, B, and Q are collineat and AQ + QB = AB
We know that geometry is kind of scary, especially with proofs and sin, cos, tan (what is that?). Don't worry, they are all here :D
def: collinear points are two or more points on the same line
def: coplanar points, lines, etc that are in the same place (3 or more)
def: midpt of a segment is the pt halfway between the endpts of the segment
on a numberline: x1 + x2 / 2
on a coordinate plane: (x1 + x2 / 2 , y1 + y2 / 2)
def: ray extends infinitely in one direction
write PQ with an arrow on top
say ray PQ
def: opposite rays have a common endpt and form a line
def: an angle is formed by two non-collinear rays with a common end pt called the vertex
review:
right angle = 90°
acute angle = less than 90°
obtuse angle = more than 90°
def: angles are congruent if & only if they have the same measure
def of an angle bisector: if PQ is the angle bisector of ∠RPS then Q lies in the interior of ∠RPS and ∠RPQ ≅ ∠QPS
def: adjacent angles are a pair of angles in the same plane with a common vertex and a common side but no common interior point
def: a linear pair is a pair of adjacent angles with non-common sides that are opposite rays
def: vertical angles are two nonadjacent angles formed by intersecting lines
thm: vertical angles are congruent
def: complementary angles are angles that have a sum of 90°
ex. if ∠A & ∠B are complementary then m∠A & m∠B added = 90°
def: supplementary angles are angles that have a sum of 180°
ex. if ∠C & ∠D are supplementary then m∠C & m∠C added = 190°
thm: the angles in a linear pair are supplementary
distance formula (use it when given two points and need to find radius, remember radius ⋅ 2 = diameter) d = sqrt((x2 - x2)2 + (y2 - y2)2)
Geometry is about working backwards in order to solve problems. Often you're given the answer to a problem and asked to demonstrate how it’s true. To do this, you must utilize geometric proofs.
This is shown with two-column proofs, take a look at the image below.
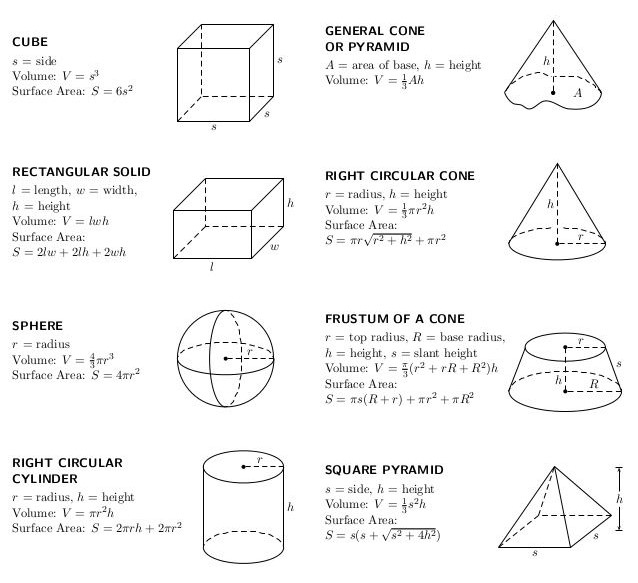
two dimensional figures: when drawn, they are flat to the paper, have two dimensions called length and width, some examples are a cirlce, a kite, and a triangle
three dimensional figures: when drawn they appear to come "off" the paper, have three dimensions called length, width, and height, some examples are a pyramid, a sphere, and a cube.