~Trigonometry~

We know that trigonometry sounds scary with all the big, fancy words. Don't worry :D. It's not as scary as it seems.

Radians and Degrees

Degrees

  • Usually a whole number and has always this symbol next to the number: °

Radians

  • An incomplete fraction that contains π
  • Can also be a number/decimal, but it will not contain a degree symbol
  • For example, do not become confused between 14 radians and 14°. They are not the same thing

Convert Radians -> Degrees and Vice Versa

Arc Length

S = rθ

Area of a Sector

A = 0.5(r2θ)

Right Triangles

This is where sin, cos, and tan come in! yay!

  • This principle is based on the coordinate plane
  • Opposite: the side that is across from the angle (y value on the coordinate plane)
  • Adjacent: the side that is below the angle (x value on the coordinate plane)
  • Hypotenuse: the slanted side
  • Each angle's corresponding side is across from it (ex. 30°'s corresponding side is 1)
  • A smaller side will have a corresponding smaller angle. A larger side will have a corresponding larger angle

The Common Triangles You Will See

  • This is the basis of the unit circle, which we will get into later of course. Make sure to remember these
  • To make it easier to memorize, remember that the smallest angle will have the smallest side
  • Most trigonometry problems involve knowing this triangle and the unit circle values
  • The 45, 45, 90 is an isoceles triangle. The 30, 60, 90 is a scalene triangle

Soh Cah Toa

  • S: sin (sine)
  • oh: stands for opposite/hypotenuse
  • C: cos (cosine)
  • ah: stands for adjacent/hypotenuse
  • T: tan (tangent)
  • oa: stands for opposite/adjacent
  • This is how you solve for the sin, cos, or tan of a triangle

How to solve for sin, cos, tan

  1. Tilt the triangle so that the desired angle is on the bottom
  2. Look above at the Soh Cah Toa cheat sheet. Use the given values of each side to find the sin/cos/tan

How to Determine if sin/cos/tan is Negative or Positive

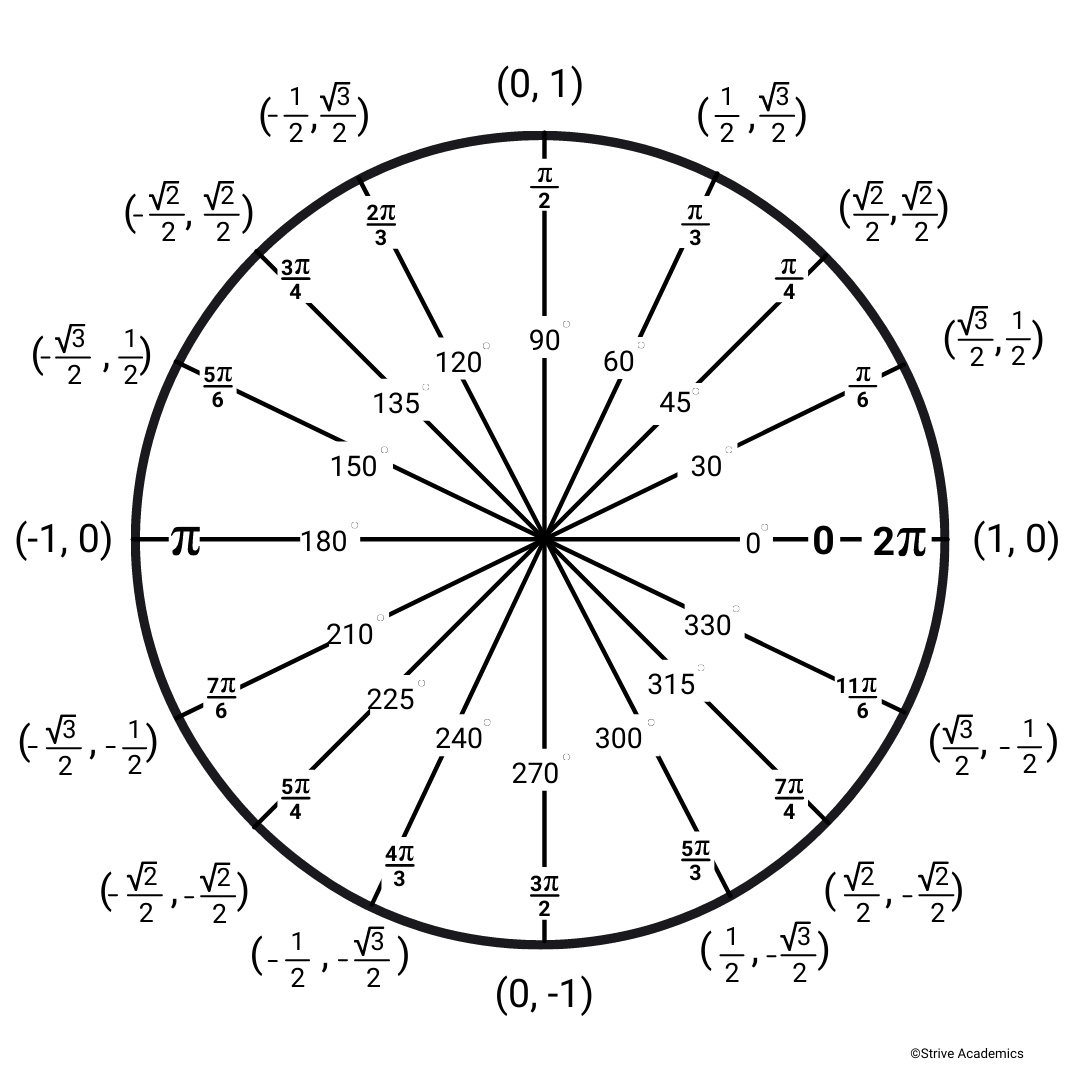
A picture of the unit circle.

A few notes

  • sin = y
  • cos = x
  • tan = sin/cos
  1. Solve for the sin/cos/tan value
  2. Check the value of the angle and think about which quadrant it would be on a coordinate plane
  3. Is the x value negative or positive (for cos)? Is the y value negative or positive (for sin)?
  4. Apply the negative/positive value to your answer
  5. For tan, find out if the values for sin and cos are positive/negative. Divide sin/cos

Reference angles

  • The angle between the given angle and the closest x axis
  • This is VERY important for the unit circle, which is why it's directly above it
  • If you know the reference angle to any angle, finding the coordinates on a unit circle will be easy

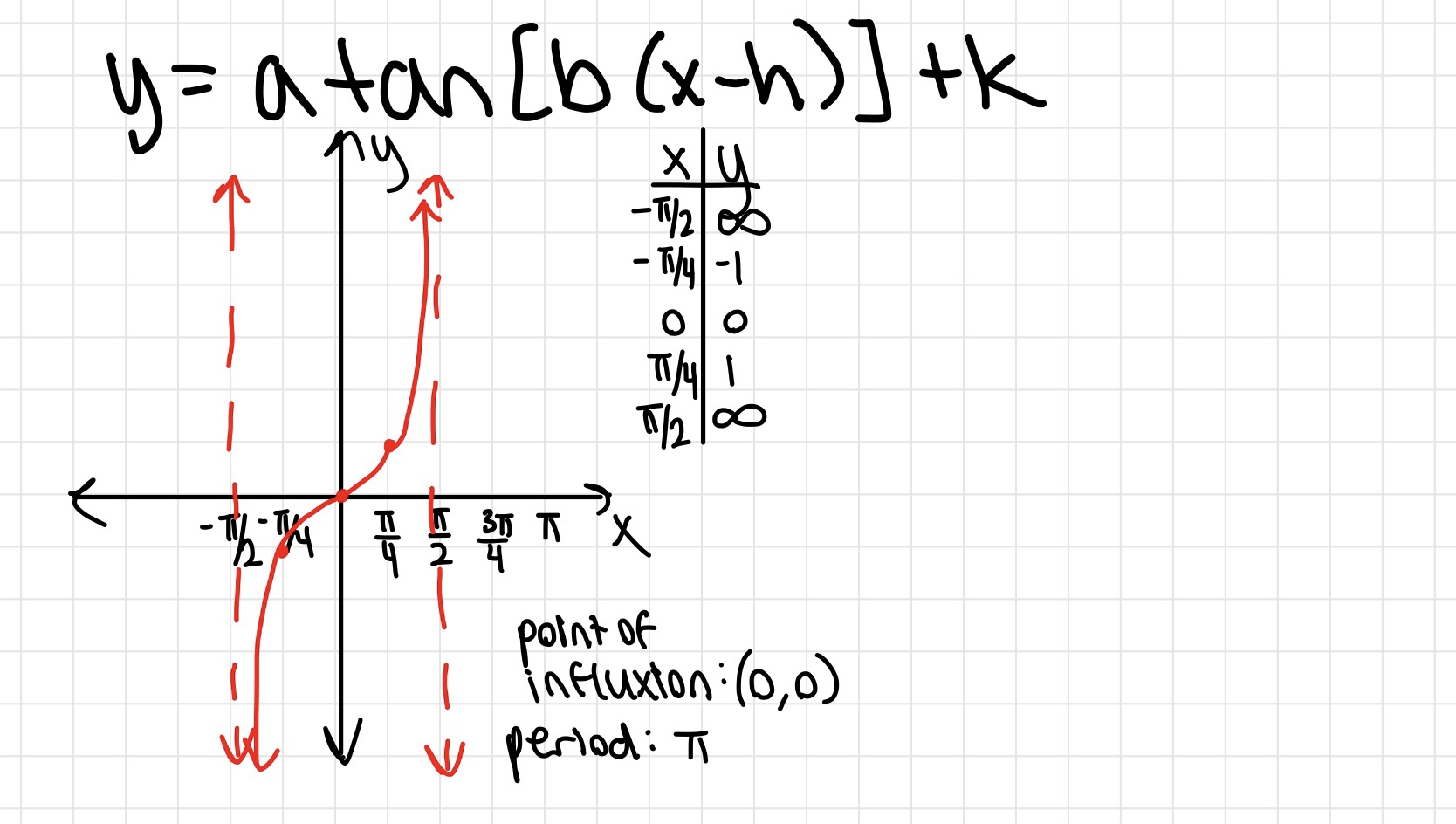
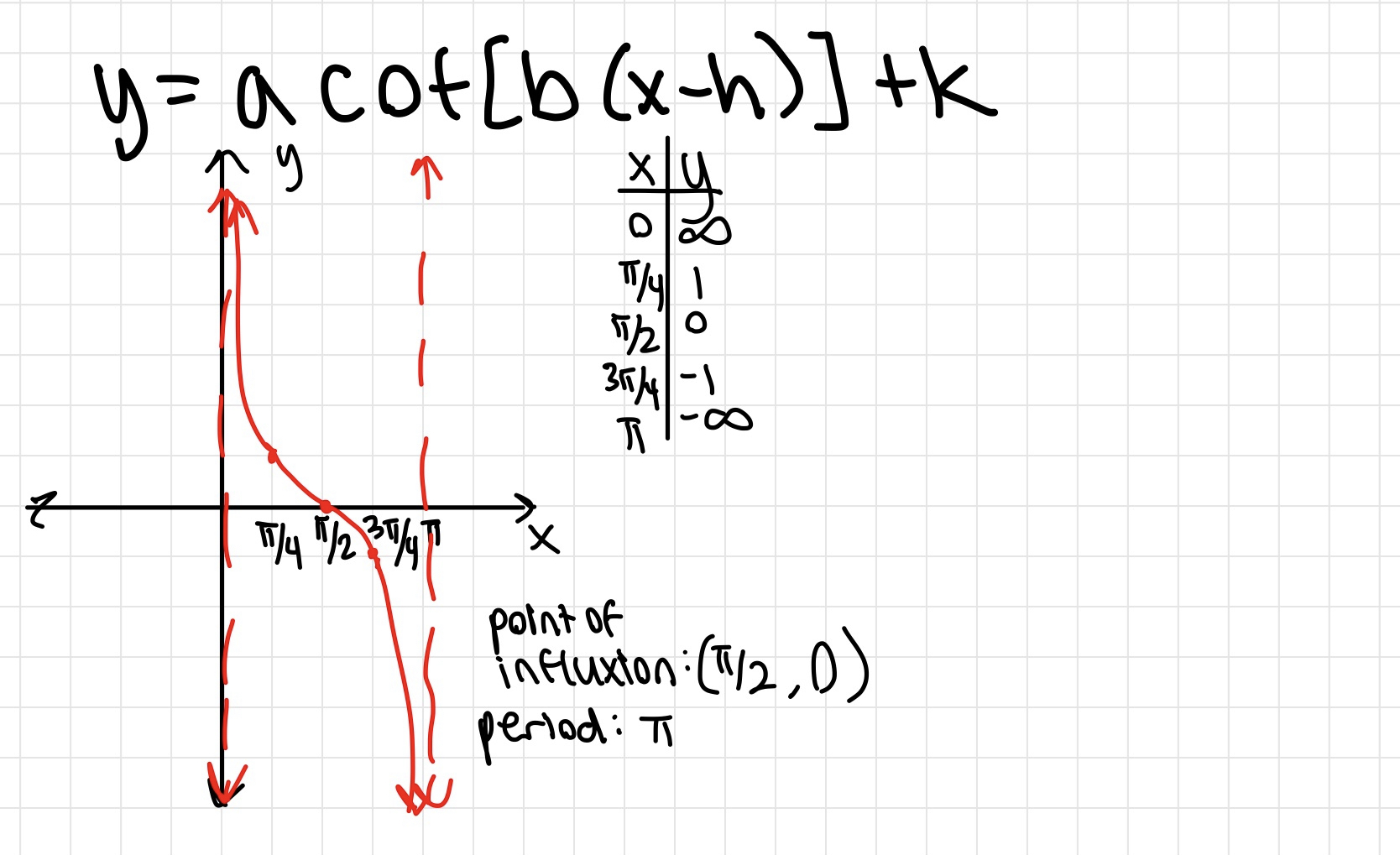
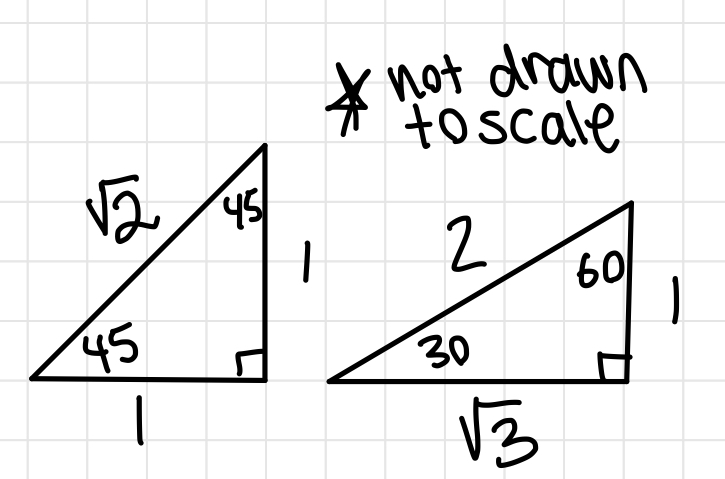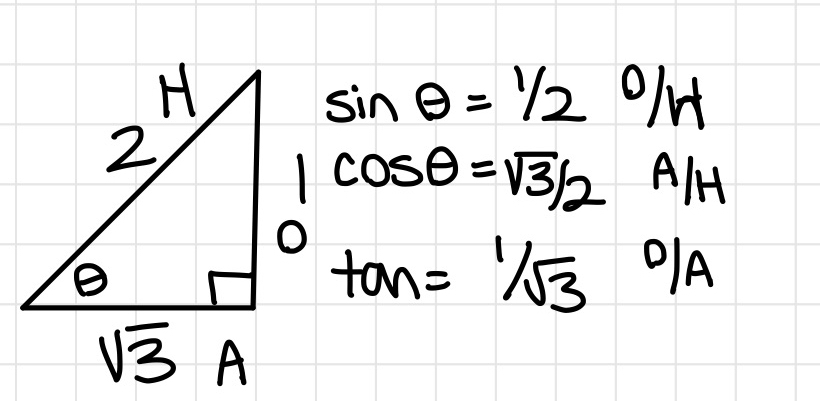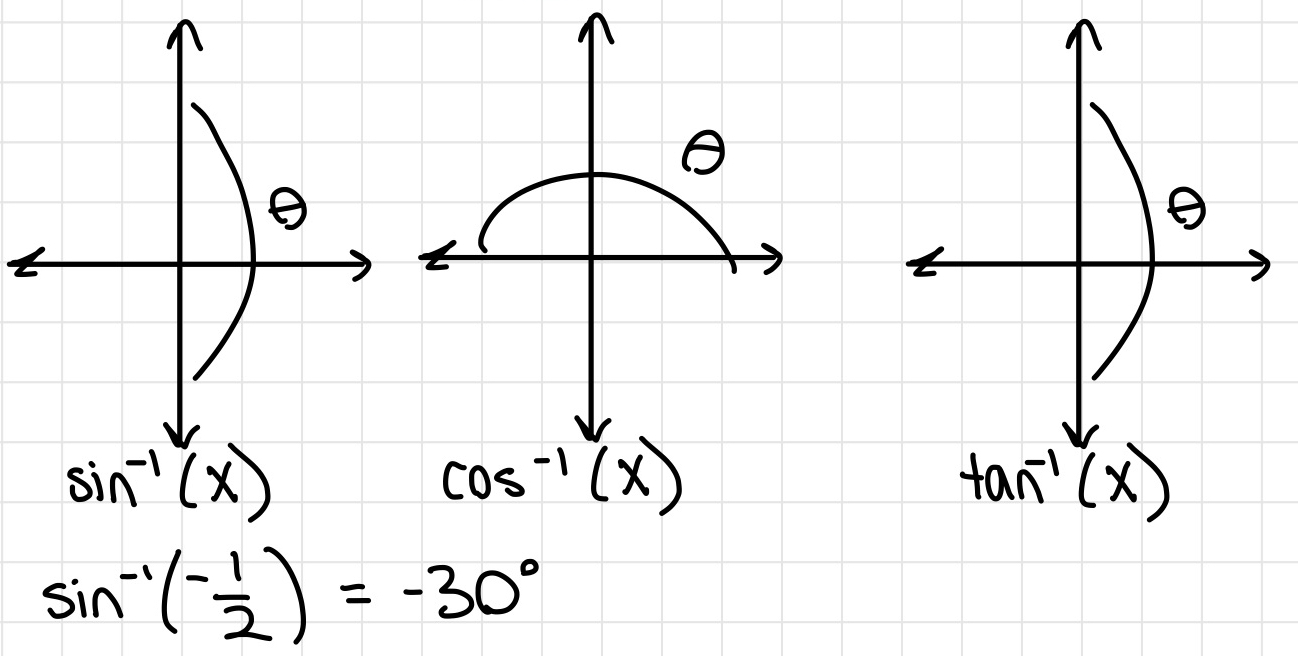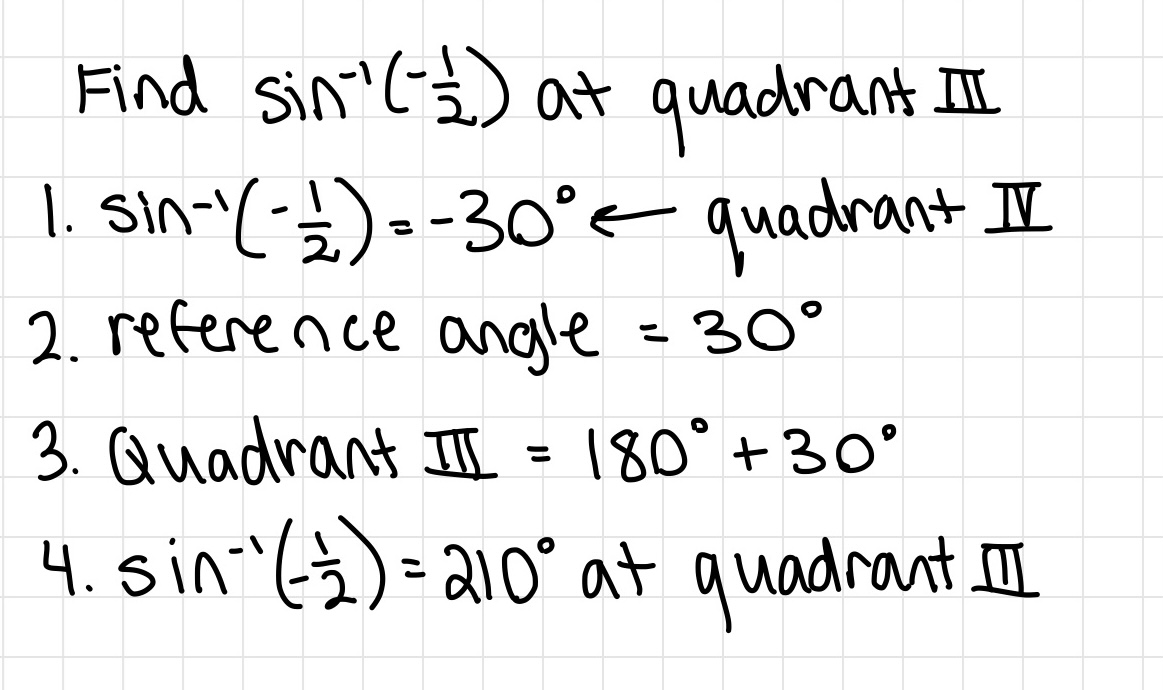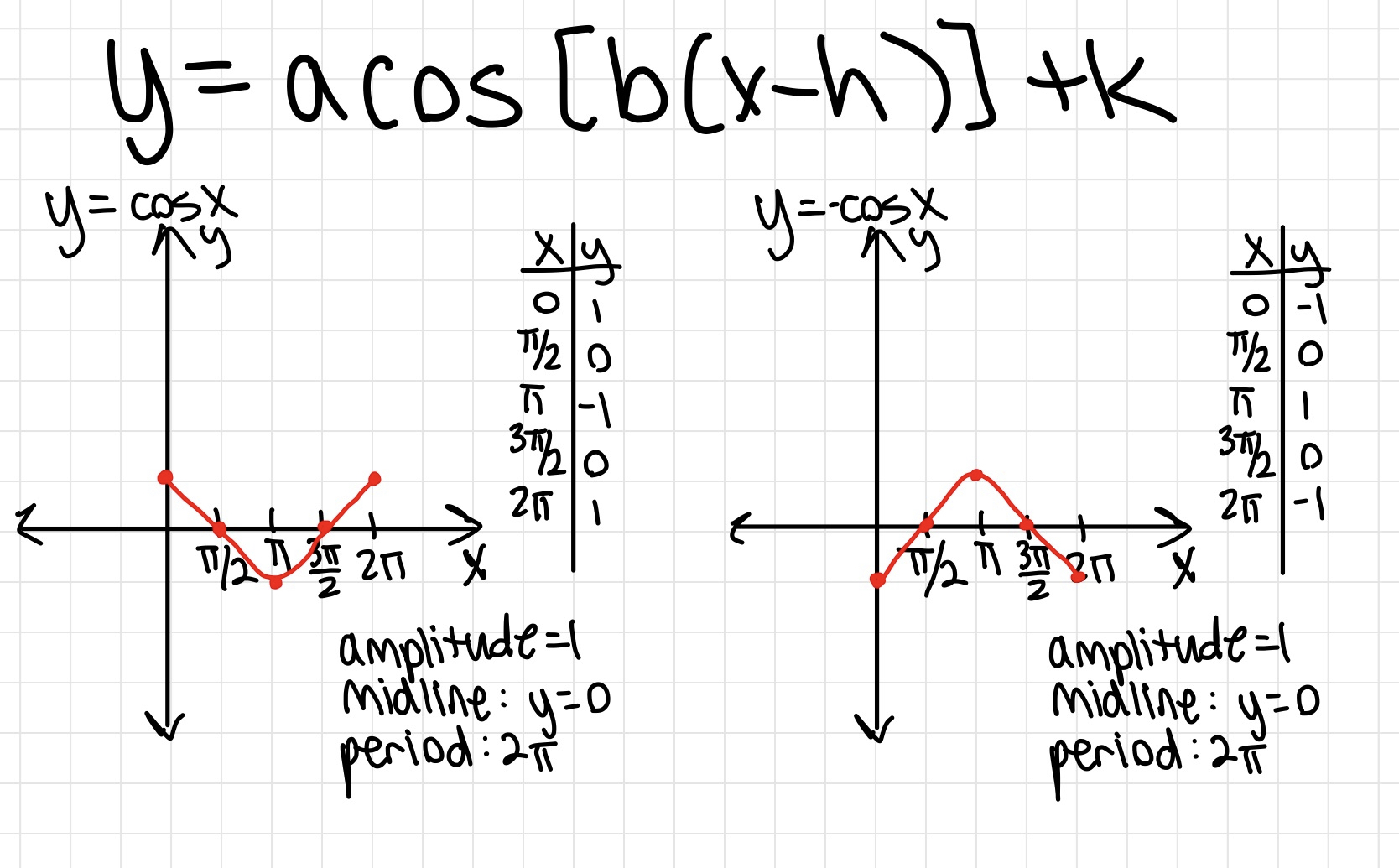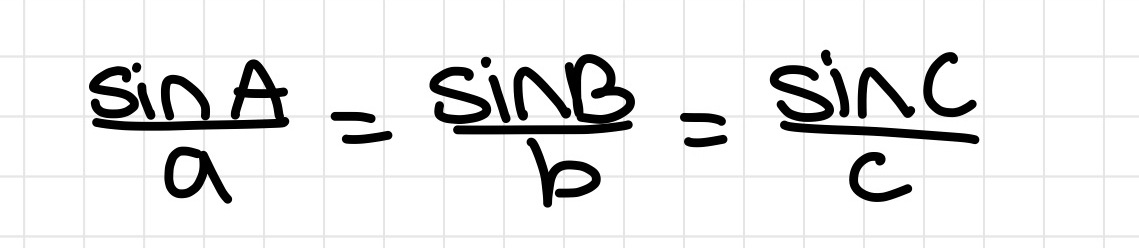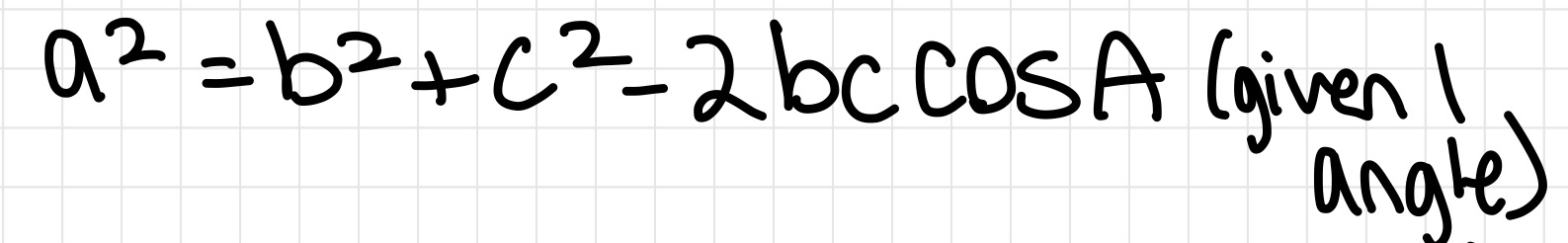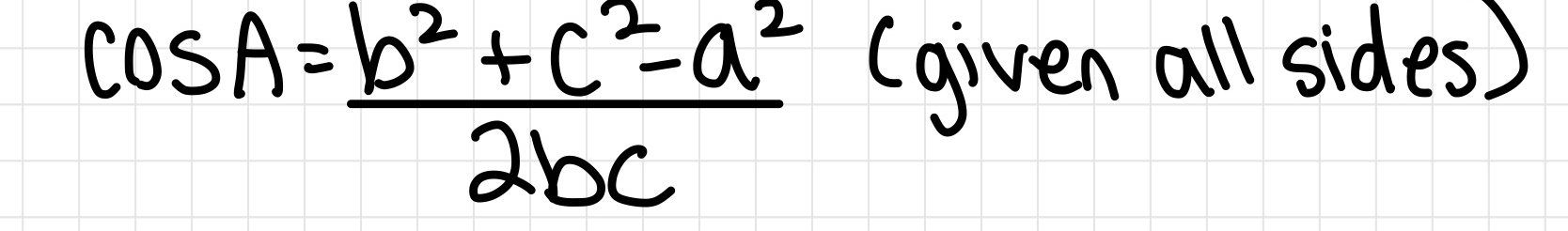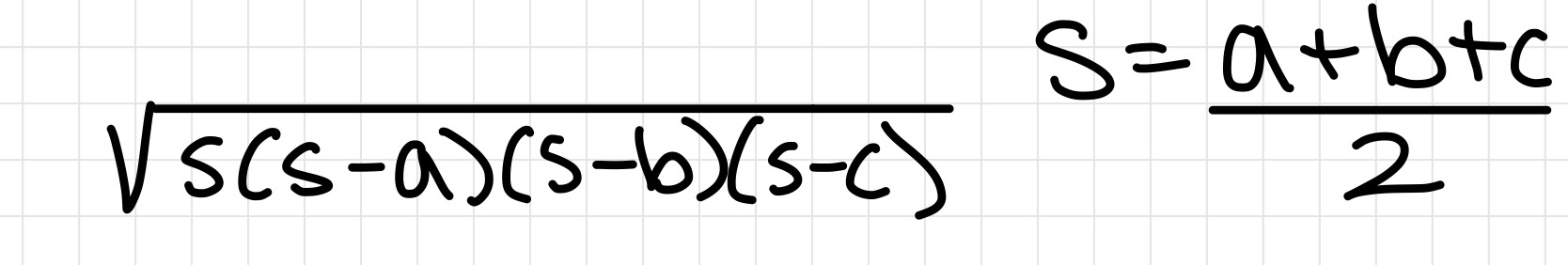Unit Circle!!!

Here are some tips + tricks to tackle the unit circle

First of all, do NOT memorize this, it is very unnecessary

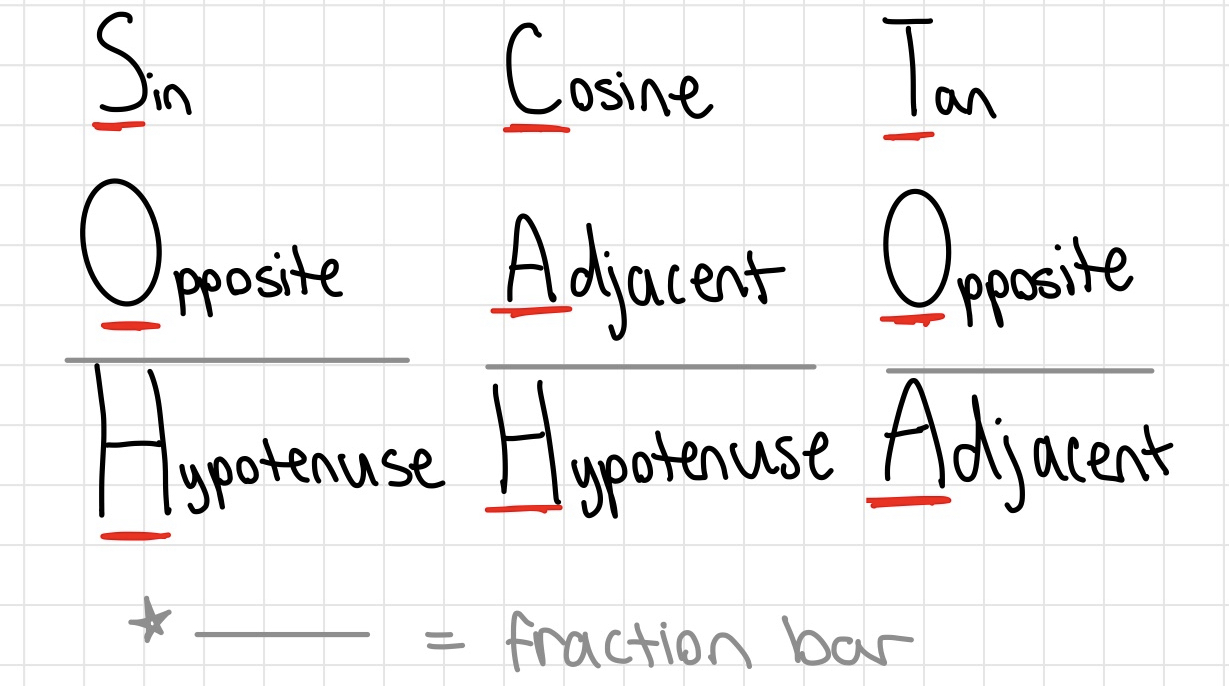
Secondly, read this if you know what sin, cos, tan, reference angles and right triangles are. If you don't, read the info above and come back later.

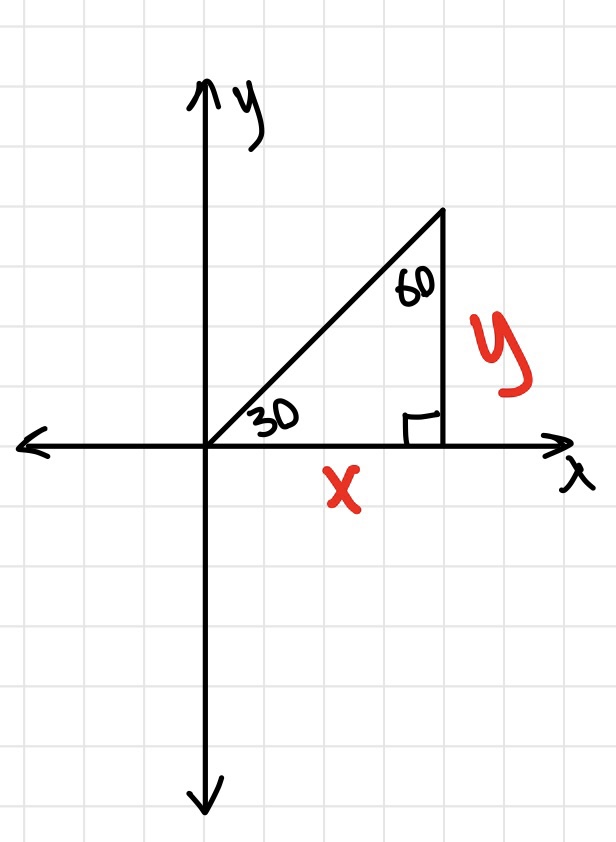
  1. Find the reference angle
  2. Find the sin, cos, or tan of the reference angle. You do this by remembering the side lengths of the 30, 60, 90 or 45, 45, 90 triangles
  3. Check which quadrant the angle is in
  4. If you are finding sin, think about if y is negative or positive in that quadrant. If you are finding cos, think about if x is negative or positive quadrant.
    If you are finding tan, find the negative/positive value of both x and y then divide sinx/cosx
  5. Switch the sign of the answer accordingly
  6. This takes some time, but don't get frustrated!

Let's Try this Together!

  1. Let's find sin 7π/6 (210°)
  2. Find the reference angle. In this case, it is π/6
  3. What is sin of π/6? If you remember the 30, 60, 90 triangle, it is 1/2
  4. Which quadrant is 7π/6 on the coordinate plane? It's in quadrant 3 where, where x and y are negative
  5. What does sin represent? Since we used the opposite angle (the y), sin represents the y value on a coordinate plane.
  6. Since y is negative in quadrant 3, we change 1/2 to -1/2

Why the angles 0, π/2, π, and 3π/2 are Different From the Right Triangle Values

For the x and y axis angles, think conceptually about the values

Keep in mind that the radius of the circle is 1

  1. When the angle is 0, the values is (1, 0) because it's the distance from the midpoint to the corners of the circle at 0°
  2. This principle is the same for the rest of the angles: When the angle is π/2 (90°), the value is (0,1) (cos π/2 = 0, sin π/2 = 1)
  3. When the angle is π (180°), the value is (-1,0) (cos π = 1, sin π = 0)
  4. When the angle is 3π/2 (270°), the value is (0,-1) (cos 3π/2 = 0, sin 3π/2 = -1)

csc, sec, cot

Trig Identities

Inverse Trig Functions

  • IS NOT 1/trig function!! It is sometimes written as arcsin, arccos, arctan
  • It is used to find the angle of a trig function using its value on a unit circle
  • A calculator only computes quadrant 1 and 4 for inverse sin and tan functions. For cos, it computes only quadrant 1 and 2.
  • If you are asked to find the inverse trig function in a quadrant out of the calculator's range, pretend the computed angle is a reference angle
  • Then, add the angle plus/minus the x axis pertaining to the reference angle

We know it sounds confusing, so here is a step by step process!

What the calculator can compute

Graphing sin, cos

A few notes:

Sin

  • Is an odd function (not symmetrical)
  • If a is positive, the function begins by going up. If a is negative, the function begins by going down
  • The first point is on the midline, second point is |a| +/- k (depending on the value of a), third is on the midline, fourth point is |a| +/- k (depending on the value of a), last point is on the midline
  • If b is negative, the negative can be taken outside of the function (odd function)

Cos

Graphing tan and cot

A few notes

Tan

Cot

Graphing csc and sec

Law of Sines

Law of cosines

Area of an oblique traingle (not a right triangle)

Heron's Formula